Szigetelő-vezető határfelület
Célkitűzés
Vizsgáljuk meg egy szigetelőben terjedő monokromatikus síkhullámnak vezető közegbe történő átlépését. Az egyszerűség miatt legyen a szigetelő közeg vákuum. A vonatkoztatási rendszert válasszuk úgy, ahogy már az átlátszó közegeknél az 5.1. ábrán látható módon tettük. Vagyis a fém felülete a z = 0 sík, továbbá a beeső síkhullám terjedési irányát megadó ![]() egységvektor felületre mezőleges komponense a z tengely, míg a felülettel párhuzamos komponense az x tengely irányába mutat. Ekkor az (z, x) sík a beesési sík. A hullámnormálisokat most is az 5.4a-c egyenletek adják meg.
egységvektor felületre mezőleges komponense a z tengely, míg a felülettel párhuzamos komponense az x tengely irányába mutat. Ekkor az (z, x) sík a beesési sík. A hullámnormálisokat most is az 5.4a-c egyenletek adják meg.
Az ármenő hullám
A Snellius-Descartes-törvény szerint
| (7.20) |
ahol ![]() a fém komplex törésmutatója. Mivel ñ komplex így a θt szintén komplex szám lesz. A jól ismert trigonometrikus azonosságot felhasználva
a fém komplex törésmutatója. Mivel ñ komplex így a θt szintén komplex szám lesz. A jól ismert trigonometrikus azonosságot felhasználva
|
|
(7.21) |
összefüggést kapjuk. Írjuk fel az
| (7.22) |
előállítást, ahol q és γ valós számok, továbbá q ≥ 0. Ezeket a paramétereket az elősző két egyenlet négyzetre emelésével nyert
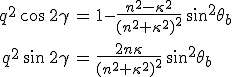 |
(7.23) |
egyenletrendszerből határozhatjuk meg. A 7.20. és 7.22. egyenleteket felhasználva a fémben terjedő hullám térfüggő fázisa
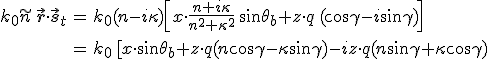 . . |
(7.24) |
Mivel a hullám amplitúdójának csökkenését a 7.22. kifejezés képzetes része határozza meg, látható, hogy az amplitúdó z irányba exponenciálisan csökken, melynek mértékét a z utáni szorzótényező határozza meg. Azok a felületek - amelyben az amplitúdó állandó - a z tengelyre merőleges síkok. A hullám fázisát a 7.22. kifejezés valós része határozza meg. Ebből leolvasható, hogy az állandó fázisú hullámfelületeket az
| (7.25) |
egyenlet határozza meg, ahol K állandó. A 7.25. egyenletből látható, hogy fázisfelületekre merőleges valós hullámnormális y koordinátája zérus, valamint az x és z koordinátája sorrendben
| (7.26) |
ahol ![]() a valós hullámnormális és a beesési merőleges által bezárt szög. Így a fázisfelületek a fém felületével
a valós hullámnormális és a beesési merőleges által bezárt szög. Így a fázisfelületek a fém felületével ![]() szöget bezáró síkok és
szöget bezáró síkok és
|
|
(7.27) |
Eredményünk azt mutatja, hogy a síkhullám azonos fázisú és azonos amplitúdójú felületei eltérőek. Az ilyen hullámot inhomogén síkhullámnak nevezzük. Egy ilyen hullámra a fázisfelületen a hullám amplitúdója nem állandó. Esetünkben egy fázisfelületen mozogva, az amplitúdó a határfelülettől mért távolsággal exponenciálisan csökken. Látható, hogy a síkhullám inhomogenitása a hullámnormális, illetve ennek következtében a θt törési szög komplex értékének a következménye.
A hullám p és s komponenseinek amplitúdóját a Fresnel-formulák adják, nb = 1 és nt = ñ helyettesítéssel kapjuk, hogy
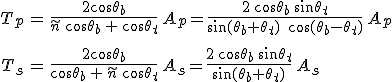 ,
,
ahol Ap és As a beeső hullám p és s komponensének amplitúdói.
A visszavert hullám
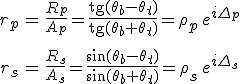 |
(7.28) |
|
|
(7.29) |
definíciókkal, ahol a 0 ≤ ψ < π/2 szöget a ![]() összefüggés definiálja. Ezek között a 7.28. egyenlet alapján
összefüggés definiálja. Ezek között a 7.28. egyenlet alapján
|
|
(7.30) |
|
|
|
|
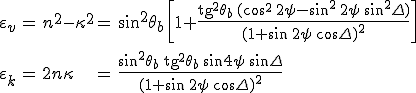 |
(7.31) |