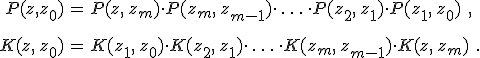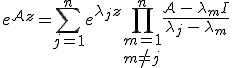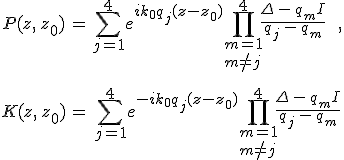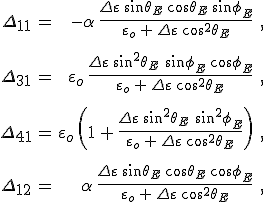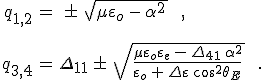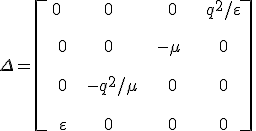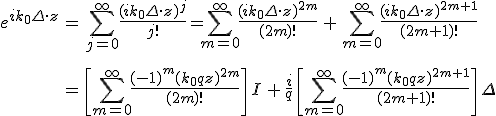A Berreman-egyenlet megoldása

A 12.15. Berreman-egyenlet az megfeleltetéssel a 6.26. egyenletnek a 4-dimenziós speciális esete. Ezért az egyenlet megoldásához egy alaprendszert, azaz a megoldások egy lineárisan független (4 elemű) rendszerét kell megtalálni. Ez általános esetben meglehetősen nehéz feladat, csak néhány speciális esetben lehet analitikus alakban kifejezni. Ezek közé tartozik az a fontos eset is mikor a Δ mátrix állandó. Ebből kiindulva pedig az alkalmazások szempontjából különösen fontos szakaszonként állandó optikai tulajdonságú rétegekből felépülő rétegrendszer is könnyen leírható.

Ha a 12.15. egyenlet Cauchy-mátrixát P(z, z₀) jelöli, akkor a 6.35. egyenlet alapján

(12.22)

összefüggés adja meg az egyenletünk megoldását, ahol . A 12.22. tulajdonsága miatt a P mátrixot gyakran propagátornak is szokás nevezni, hiszen a z₀ és a z síkok közötti terjedést írja le. A reflexióra és transzmisszióra vonatkozó Jones-féle mátrix elemeinek (reflexiós és transzmissziós tényezőknek) kiszámolásához a Cauchy-mátrix inverzére, a

(12.23)

a karakterisztikus mátrixra van szükség. A karakterisztikus mátrixot az irodalomban szokás részleges átviteli mátrixnak is nevezni (angolul partial transfer matrix). A karakterisztikus mátrix a z és z₀ helyek közötti összefüggést írja le, hiszen a definícióból és a 12.12. egyenletből

(12.24)

reláció következik. Az izotróp rétegrendszerhez hasonlóan most is fennáll, hogy ha a z₀ és z síkok közötti réteget a helyen lévő síkokkal m darab elemi rétegre bontjuk fel, akkor a rendszer Cauchy- illetve karakterisztikus mátrixa az elemi rétegek mátrixainak szorzatával számítható ki:

(12.25)

A 12.25. alapvető tulajdonság teszi lehetővé, az alkalmazásoknál igen lényeges szakaszonként homogén közeg egyszerű tárgyalását.

A 6.39. egyenlet és az megfeleltetés alapján a homogén közeg Cauchy- illetve karakterisztikus mátrixát az

és

(12.26)

összefüggések adják meg. Amint azt már említettük, a mátrix exponenciális függvény a Cayley-Hamilton-tétel következményeként - a 6.42. egyenlet alapján - a 4×4-es mátrix exponenciális függvénye  3-ad fokú polinomjaként is kifejezhető. A polinom együtthatóit a 6.43. lineáris egyenletrendszer megoldásával kaphatjuk meg. Bizonyítás nélkül, a teljesség kedvéért közöljük, hogy az ún. Sylvester-féle kifejtési tétel szerint, amennyiben az n×n-es mátrix λ_m sajátértékei egyszeresek (m = 1, 2, …, n), akkor az interpolációs polinom az

(12.27)

alakban adható meg, ahol I az n×n-es egység mátrix. Ezért amennyiben a Berreman-mátrix sajátértékei nem elfajultak, akkor a homogén anizotróp lemez Cauchy- illetve karakterisztikus mátrixa a

(12.28)

összefüggésekkel számolható ki, ahol q_m a Berreman-mátrix sajátértékeit (m = 1, 2, 3, 4), I a 4×4-es egység mátrixot jelöli. Az összegen belüli szorzatokat elvégezve, és Δ hatványait kiemelve megkaphatjuk a polinom előállítás r₀, r₁, r₂, r₃ együtthatóit. Többszörös sajátértékek esetén 12.28. egyenletben 0/0 típusú kifejezések lépnek fel, melyek határértéke például a L'Hospital szabállyal kiszámolható. A 6.43. lineáris egyenletrendszer egyaránt alkalmazható elfajult és nem-elfajult sajátértékek esetén.

A fentiek szerint a karakterisztikus mátrix kiszámításának első lépése a Berreman-mátrix sajátértékeinek a meghatározása. A lineáris algebrából ismert, hogy a sajátértékek Δ karakterisztikus polinomjának a gyökei, azaz a

(12.29)

egyenlet megoldásai. Mivel Δ 4×4-es mátrix, 12.29. negyedfokú algebrai egyenlet, amely viszonylag egyszerűen megoldható. Egy negyedfokú polinom két másodfokú polinom szorzatára alakítható át (faktorizálható) egy köbös, ún rezolvens polinom gyökeinek meghatározásával. Harmadfokú egyenletek megoldására pedig analitikus összefüggések ismertek. A faktorizáció ismeretében a gyökök egyszerűen kiszámíthatók a két másodfokú tényezőre vonatkozó, jól ismert megoldóképletből. Az elmondottak alapján a sajátértékeket, a 12.29. egyenlet gyökeit (viszonylag) egyszerűen határozhatjuk meg. A sajátértékek ismeretében a 12.28. formula, vagy - a 6.43. lineáris egyenletrendszer megoldásával - a 6.45. összefüggés szolgáltatja a karakterisztikus mátrixot, Δ harmadfokú polinomjaként.

Az alkalmazásoknál különösen fontos egytengelyű kristályok esetén a 12.15., a 12.20. és a 12.21. egyenleteket felhasználva, a Berreman-mátrix független elemeit a

(12.30)

összefüggésekkel számolhatjuk ki. Erre a fontos esetre a sajátértékek is analitikusan kiszámíthatók [5]. A 12.30. összefüggéseket felhasználva a karakterisztikus polinom két másodfokú polinom tényezőre faktorizálható. A másodfokú tényezők

(12.31)

gyökei adják meg a keresett sajátértékeket.

Homogén izotróp közeg esetén , amiből . Így a 12.15. és 12.30. egyenletek alapján a Berreman-mátrixot a

(12.32)

összefüggés adja meg, ahol

,

(12.33)

a lemez törésmutatója és θ a törési szög. Az utolsó átalakításnál az Snellius-Descartes-törvényt és trigonometrikus azonosságot használtunk fel. A sajátértékre a 12.30. és 12.31. összefüggésekből

és

(12.34)

egyenleteket kapjuk. A 12.32. összefüggésekből Δ páros és páratlan hatványait az

és

(12.35)

egyenletekkel fejezhetjük ki (m = 0, 1, 2, …), amiből az exponenciális függvényt, - a hatványsorát megvizsgálva, - az

(12.36)

alakba írhatjuk fel, ahol I a 4×4 egység mátrix. Így a 12.26. egyenlet alapján a homogén izotróp közeg Cauchy-, illetve karakterisztikus mátrixát a

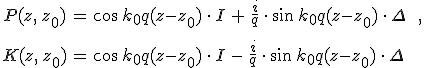(12.37)

kifejezések adják meg. A 12.32. összefüggésbeli Δ, és az egység mátrixot behelyettesítve az

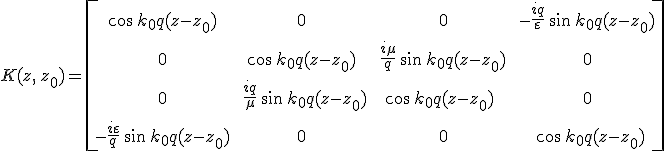(12.38)

egyenletet kapjuk a karakterisztikus mátrixra.