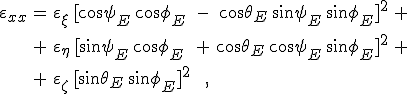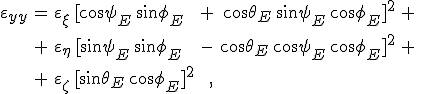Berreman-egyenlet

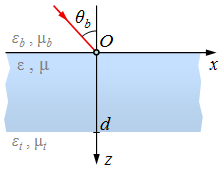
	12.1. ábra. Anizotróp rétegelt lemezre beeső síkhullám vissza-verődésének és áthaladásának vizsgálatánál használt koordináta-rendszer és jelölések.

Tegyük fel, hogy homogén izotróp közegekkel körülvett, sík lapokkal határolt, a síkokra merőlegesen rétegezett, elektromos szempontból anizotróp lemezre egy monokromatikus síkhullám esik. A koordináta-rendszert vegyük fel a szokásos módon, azaz legyen a beesési sík az x és a z tengelyek által kifeszített sík, és a lemez helyezkedjen el az x = 0 és z = d síkok között, így a rétegezett anizotróp lemez vastagsága d. A beeső hullám a z < 0 térrészből érkezik a lemezre. Keressük a lemez visszaverődésre és átengedésére vonatkozó Jones-féle mátrixait. A Fresnel-formulához hasonlóan jelölje  és  a beeső, és a visszavert, valamint és az átengedett hullámok térerősségeinek p illetve s irányú komponenseit. Az amplitúdók között fennállnak az

és

(12.1)

összefüggések, ahol

és

(12.2)

a visszaverődésre illetve az átengedésre vonatkozó Jones-mátrixok. Töltés- és árammentes esetben, monokromatikus függést feltételezve az M-1 és M-2 egyenletek az

és

(12.3)

összefüggésekre vezetnek, ahol E, D, H és B vektorok a térmennyiségek helyfüggő részét jelölik. Az összefüggéseket célszerű tömör, mátrixos alakban felírni. Azon célból, hogy az SI rendszer optikai szempontból gyakran nem igazán előnyös használatából származó nehézségeket elkerüljük, a 12.3. első egyenletét szorozzuk meg a vákuum Z₀ hullámimpedanciájával. Ezzel a megjegyzéssel a 12.3 egyenleteket szimbolikusan az

(12.4)

formában írhatjuk fel, ahol R a 3×3-as zérus mátrixokból a  szimbolikus operátorból felépülő blokk mátrixot jelöli. Az 1.3. és az 1.7. anyagegyenleteket pedig az

(12.5)

alakba írhatjuk fel együttesen, ahol c a vákuumbeli fénysebesség, ε a relatív dielektromos tenzor mátrixa, μ a relatív permeabilitás és I a 3×3-as egységmátrix. Ha bevezetjük a

(12.6)

6-dimenziós vektort, akkor a 12.4. és a 12.5. egyenletek együttesen a

(12.7)

eredményre vezetnek, ahol a vákuumbeli hullámszám és a T felső index a transzponálást jelöli. A 12.7. egyenletben mutatkozik meg a Z₀·H mennyiség bevezetésének az előnye: a Γ vektor komponensei azonos dimenziójú mennyiségek, ennek következtében az M mátrix dimenziómentes, ahogy az 12.5. definiáló egyenletből is látható. A már vizsgált izotróp esethez hasonló megoldást keresünk. A beeső hullám szimmetriája miatt kézenfekvő feltevés, hogy a térmennyiségek függetlenek az y koordinátától, továbbá az x irányú függés a 6.14. és a 6.15. egyenletekkel azonos típusú, azaz alakú, ahol a 6.55. egyenlethez hasonlóan

(12.8)

állandó, n_b a törésmutató a lemez felett (z < 0), θ_b a beesési szög. Az függéssel a két határfelületen a peremfeltételek is egyszerűen teljesíthetők. Az elmondottakat figyelembe véve az R operátort derékszögű koordinátákkal kifejezve az y szerinti parciális derivált zérussal, a x szerinti parciális derivált  számmal való szorzással ekvivalens, azaz explicit módon kiírva a műveleteket

(12.9)

alakba írhatjuk. Az R mátrix 3. és 6. sorában nincsen differenciáloperátor, és csak egy zérustól különböző elem van. Ennek az a következménye, hogy a 12.7. egyenletrendszer 3. és 6. egyenletei az  mennyiséggel való egyszerűsítés után a

(12.10)

lineáris egyenletekre vezetnek. Ezen egyenletrendszerből a Γ₃ = E_z és Γ₆ = Z₀·H_z változók, azaz a térerősségek z komponensei kifejezhető a maradék,  Γ₁,  Γ₂,  Γ₄ és  Γ₅ változók, vagyis a térerősségek x és y komponenseinek segítségével. Ezért vezessük be a

(12.11)

definícióval a 4-dimenziós Ψ vektort. A Γ₃ és a Γ₆ változókat kifejezhetjük a Ψ vektor elemeinek lineáris kombinációjaként. Ezeket az előállításokat a 12.7. egyenletrendszer 1., 2., 4. és 5. egyenletébe helyettesítve, és rendezve az

(12.12)

egyenletrendszerhez juthatunk. A jobb oldalon lévő S_mj együtthatók az M mátrix elemeitől függnek, ezek explicit alakját itt nem adjuk meg. Csak a számolás alkalmazásoknál fontos végeredményét közöljük majd. Az S = [S_mj] mátrix segítségével a 12.12. egyenletrendszer az

(12.13)

tömör alakba írható. Az egyenlet bal oldalán álló vektort is kifejezhetjük a

(12.14)

nyilvánvaló összefüggéssel, amit a a 12.13. egyenletbe helyettesítve és az így kapott kifejezést a T mátrix inverzével balról szorozva a

(12.15)

Berreman-féle egyenletethez jutunk [1-5], ahol

(12.14)

az ún. Berreman-féle mátrix, továbbá kihasználtuk, hogy a T mátrix inverze magával a T mátrixszal azonos , A Berreman-mátrix explicit alakjára, az M mátrix definícióját felhasználva, egyszerű (de kissé hosszadalmas) számolás után

(12.15a)

formula adódik, ahol α a beeső hullám által meghatározott numerikus apertúra, amit a 12.8. egyenlet ad meg. Optikában általában az anyagok nem mágnesesek, így gyakran μ = 1 feltétel áll fenn. Ne feledjük, hogy a relatív dielektromos tenzor szimmetrikus, azaz fennáll a összefüggés (m, j = x, y. z). Az ε tenzor szimmetriáját figyelembe véve a Berreman-mátrix a

(12.15b)

alakba írható fel, mivel bizonyos elemei nem függetlenek. A hullámterjedés leírására használt koordináta-rendszer és a dielektromos főtengely-rendszer természetesen nem azonos. A két koordináta-rendszer egymáshoz való állását a merev testek helyzetének leírásánál is használt Euler-féle szögekkel írhatjuk le. A dielektromos tenzor két koordináta-rendszer közötti kapcsolatát alább adjuk meg. A térerősségeket a 12.15. Berreman-egyenlet megoldásából számíthatjuk ki. Az egyenlet megoldását szintén hamarosan tárgyaljuk.

A 11. fejezetben és az előbbi gondolatmenetben is csak átlátszó kristályokkal foglalkoztunk. Érdemes megjegyezni, hogy a formalizmus kiterjeszthető [6] olyan elnyelő kristályokra is, melyeknél a szimmetria tulajdonságok meghatározzák a főtengelyek irányait. Az ilyen kristályokban az ε (relatív) dielektromos tenzor és σ vezetőképesség tenzor közös főtengelyrendszerrel rendelkezik [6]. Bevezetve az iztotróp esethez hasonlóan az

(12.16)

komplex dielektromos tenzort, az előző fejezetben megismert egyenletek nagy része továbbra is érvényben marad. Például továbbra is formálisan érvényes Fresnel-féle sebességi egyenlet, azonban ennek a gyökei komplexek, így a fizikai interpretációjuk is kissé módosul [6]. Lényeges különbség még, hogy a l1.32. illetve a 11.35. homogén lineáris egyenletekben az szorzótényezők komplexek, amelynek következtében a két sebességhez tartozó rezgések komponenseinek aránya is komplex. Ez azt jelenti, hogy a rezgés ellipszisben poláros. Másrészt D vektornak lesz az s hullámnormális irányába mutató komponense is [6]. Gyengén elnyelő kristályokra ezek az eltérések kicsik. A rezgési viszonyok hasonlóak a nem-elnyelő kristályokéhoz, csak a hullámok a terjedés során csillapodnak.

Jegyezzük meg, hogy a komplex dielektromos állandó és komplex törésmutató bevezetésénél használt időfüggés helyett ezúttal az alakot használtuk, ezért a 12.16. egyenletben a komplex dielektromos állandóra (és törésmutatóra is) a már levezetett kifejezések komplex konjugáltját kell használni.

	12.2. ábra. A síkhullám terjedésének a vizsgálatánál használt (x, y, z) koordináta-rendszer és a (ξ, η, ζ,) dielektromos fő- tengely-rendszer egymáshoz viszonyított helyzetét az Euler-féle szögekkel adhatjuk meg.

Jelölje (ξ, η, ζ) a dielektromos főtengely-rendszerbeli koordinátákat. Ebben a koordináta-rendszerben az ε relatív dielektromos tenzor mátrixa diagonális és a főátlóban az fődielektromos állandók állnak. Ha a (x, y, z) koordináta-rendszer és a főtengely-rendszer egymáshoz viszonyított helyzetét a 12.2. ábrán látható módon értelmezett Euler-szögek adják meg, akkor a dielektromos tenzor (x, y, z) koordináta-rendszerbeli mátrixát az

(12.17)

egyenletből számíthatjuk ki, ahol a mátrixok felső T indexe a  transzponálást jelöli, az ε tenzor (ξ, η, ζ) főtengely-rendszerbeli diagonális mátrixa, továbbá

,

(12.18)

amiből látható, hogy az A transzformáció három, az  Euler-szögekkel történő, egymást követő forgatás. Könnyen megmutatható, hogy az A mátrix ortogonális, azaz tulajdonsággal bír. A 12.17. és 12.18. egyenletbeli szorzásokat elvégezve az

	(12.19a)
	(12.19b)
	(12.19c)
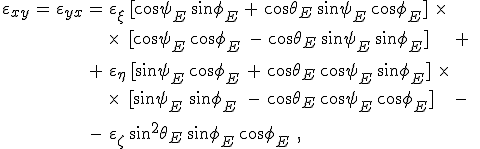	(12.19d)
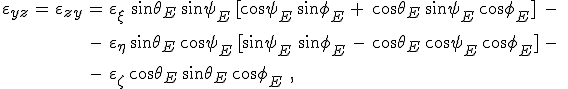	(12.19e)
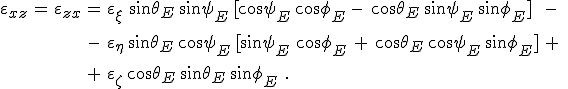	(12.19f)

formulák adódnak a dielektromos mátrix elemeire. Egytengelyű kristály esetén ezek a formulák lényegesen egyszerűsíthetők. Ha a szokásos módon az optikai tengely a ζ tengely irányába mutat, és az

,         és

(12.20)

jelöléseket bevezetjük, akkor a 12.19. egyenleteket az

	(12.21a)
	(12.21b)
	(12.21c)
	(12.21d)
	(12.21e)
	(12.21f)

alakra hozhatjuk.
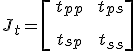
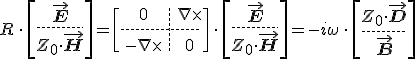
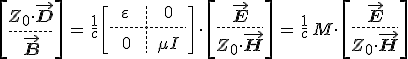
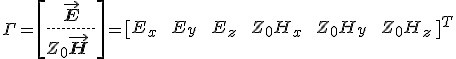
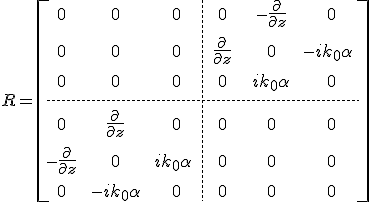
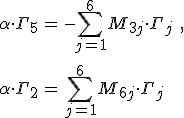
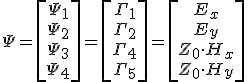
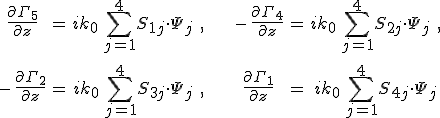
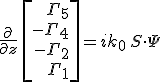
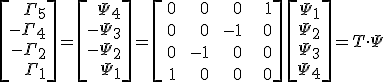
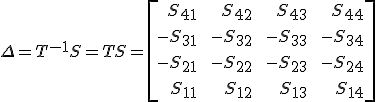
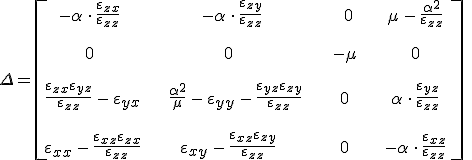
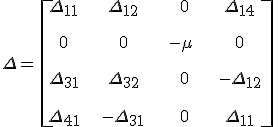
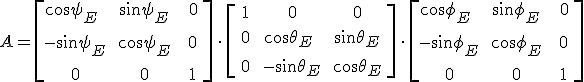