Müller-féle mátrix
A bevezetőben már említettük, hogy az optikai elemeken áthaladó fény Stoke-féle paramétereinek változása lineáris összefüggéssel írható le, melyet célszerű a
![]()
tömör mátrixos alakban felírni, ahol a ![]() a belépő,
a belépő, ![]() pedig a kilépő fény Stokes-féle vektora. Az M mátrixot az optikai rendszer Müller-féle mátrixának nevezzük.
pedig a kilépő fény Stokes-féle vektora. Az M mátrixot az optikai rendszer Müller-féle mátrixának nevezzük.
A Stokes-féle vektor transzformációja a koordináta-rendszer forgatásakor
Mielőtt néhány konkrét optikai rendszernek a Stokes-vektorra gyakorolt hatásával foglalkoznánk, célszerű megvizsgálni, hogy miként változnak a Stokes-vektor komponensei a koordináta-rendszer forgatásakor. Ezen transzformáció ismeretében a számolások egyszerűbben elvégezhetők. Jelölje a komplex térerősség komponenseit Ux és Uy az (x, y), míg Uξ és Uη a (ξ, η) koordináta-rendszerekben, ahol az utóbbi tengelyei α szöggel vannak elfogatva, így a 4.6. egyenlet alapján
|
|
(4.24) |
összefüggés áll fenn a térerősség komponensei között. A 4.20. egyenlet alapján az elforgatott koordináta-rendszerben a Stokes-vektor elemeit az
|
|
(4.25) |
formulákból számolhatjuk ki. A 4.24. egyenleteket a 4.25. képletekbe helyettesítve és a szögfüggvények négyzetösszegeire valamint a kétszeres szögekre vonatkozó azonosságokat felhasználva
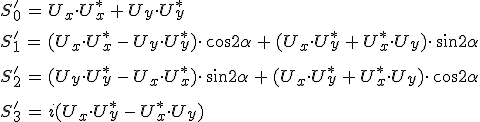 |
(4.26) |
adódik. A Stokes-paraméterek 4.20. egyenletbeli komplex előállítását ismét felhasználva
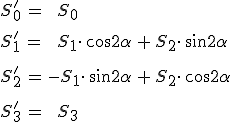 |
(4.27) |
eredményhez jutunk, ami azt mutatja, hogy az elforgatott rendszerbeli paraméterek az eredeti paraméterek lineáris kombinációi. Így 4.27. egyenletet
| (4.28) |
mátrixos formában is felírhatjuk, ahol
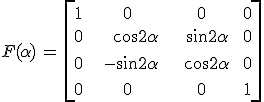 |
(4.29) |
a mátrix írja le a koordináta rendszer elforgatásának a hatását. A számolásoknál sokszor szükség van, hogy az elforgatott rendszerből visszatérjünk az eredeti rendszerbe. Ezt a transzformációt nyilván az F(α) mátrix inverze írja le. Könnyű belátni, hogy ![]() .
.
Ideális polarizátor
Legyen a polarizátor átviteli tengelye α szöggel elforgatva. Először azt vizsgáljuk meg, hogy ebben az elforgatott koordináta-rendszerben hogyan írható le a polarizátor hatása. Ennek ismeretében a forgatási transzformációval az általános esetet is könnyen megkaphatjuk. Az ideális polarizátor a ξ tengely irányába eső térerősséget változatlanul átengedi, míg az η tengely irányába eső térerősség komponenst teljesen elnyeli, így a belépő és a kilépő fény térerősségei között az
| |
(4.30) |
kapcsolat áll fenn, ahol a felülhúzás jelöli a kilépő fényre vonatkozó mennyiségeket. A 4.20. egyenlet alapján a Stokes-paraméterekre az
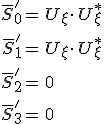 |
(4.31) |
összefüggések adódnak, amely a 4.1. táblázat első sora alapján összhangban van azzal az elvárással, hogy a kilépő fény ξ irányban lineárisan poláros. A jobb oldalon lévő mennyiséget viszont ki tudjuk fejezni a Stokes-féle paraméterekkel: a 4.20. egyenletből
| (4.32) |
Amit felhasználva 4.31. formulát a kilépő és a belépő fény Stokes-vektorai közötti kapcsolatot az
| (4.33) |
összefüggés írja le a polarizátorhoz rögzített vonatkoztatási rendszerben, ahol
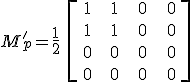 |
(4.34) |
Mivel az (x, y) és (ξ, η) vonatkoztatási rendszerbeli Stokes-vektorok között fennáll az
| (4.35) |
kapcsolat, melyeket a 4.33. egyenletet helyettesítve és F(α) inverzével balról szorozva
| (4.36) |
összefüggést kapjuk. A mátrix szorzásokat elvégezve, az x tengelyhez képest α szöggel elforgatott ideális polarizátor Müller-féle mátrixára az
|
|
(4.37) |
eredmény adódik. Természetesen pontosan ugyanez az eredmény adódik, ha a 4.11. egyenletekkel kiszámítjuk a polarizátorból kilépő fény térerősségét és ebből a 4.20. összefüggések alapján közvetlenül meghatározzuk a Stokes-féle paramétereket, csak ekkor a számolás kicsit hosszabb. A forgatási transzformáció vizsgálatának éppen a számolások egyszerűsítése volt az egyik lényeges célja.
Ideális kompenzátor
A vizsgálatot az előző esethez hasonlóan, most is célszerű úgy elvégezi, hogy először meghatározzuk a kompenzátorhoz rögzített vonatkoztatási rendszerben a Müller-mátrixot, majd a forgatási transzformációt alkalmazzuk. Ha a ξ tengely a gyors tengely és az η tengely a lassú tengely, akkor a 4.13. Jones-mátrixból rögtön következik, hogy a kilépő és a belépő fény térerősségei között az
| |
(4.38) |
összefüggések állnak fenn, ahol δ a kompenzátor által bevezetett fáziskésés. Ezeket a Stokes-féle paraméterek 4.20. komplex előállításába helyettesítve és az Euler-féle formulákat felhasználva egyszerű számolással kapjuk, hogy
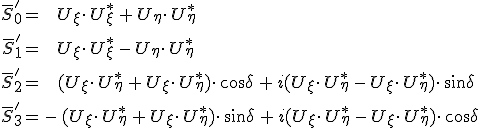 |
(4.39) |
a kilépő fény Stokes-féle paramétereit a kompenzátorhoz rögzített rendszerben. Látható, hogy az egyenletekbe ismét megjelentek a belépő fény Stokes-féle paraméterei a 4.20. komplex alakjukban. Így
|
|
(4.40) |
A laboratóriumi rendszerbe a polarizátornál látott módon térhetünk át, vagyis a most is fennálló 4.35. relációkat alkalmazva teljesül az
|
|
(4.41) |
egyenlet, ahol a mátrixok behelyettesítésével
|
|
(4.42) |
adódik a Müller-mátrixra. Az alkalmazásoknál különösen fontos λ/4-es lemez esetén δ = π/2, így ennek Müller-féle mátrixa
|
|
(4.43) |
Hasonlóan a λ/2-es lemez esetén δ = π értékkel
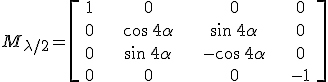 |
(4.44) |
adódik a 4.42. egyenlet speciális eseteként.
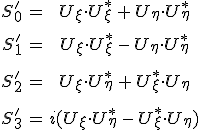
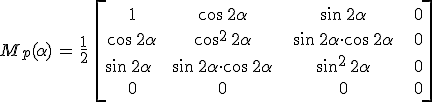
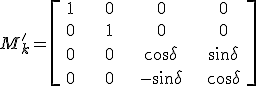 .
.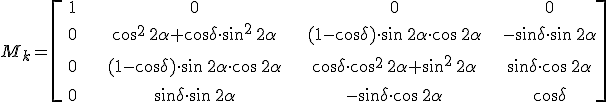
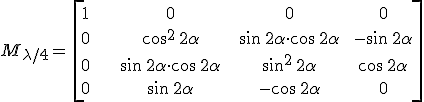 .
.