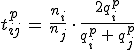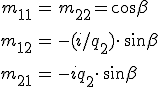Homogén sík-párhuzamos lemez
 |
|
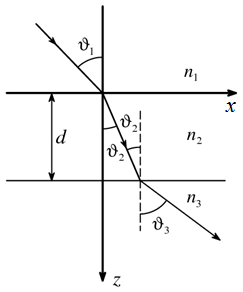
| 6.2. ábra. Sík-párhuzamos lemez beesési síkbeli metszete. |
Gyakorlatban gyakran előfordul és ezért nagyon fontos eset az, amikor a fény a két oldalról homogén közegekkel határolt homogén sík-párhuzamos lemezre esik. Ez nyilván olyan speciális esete az előző alfejezetben vizsgált problémának, mikor a lemez optikai jellemzői állandók. Így az eddig levezetett formulákat alkalmazhatjuk. Most a lemez felett 1, a lemezben 2, míg a lemez alatt 3 indexszel jelöljük a fizikai mennyiségeket, ahogy az a 6.2. ábrán is látható. A terjedés során
|
|
(6.70) |
mennyiség állandó, amely nyilván nem más, mint a jól ismert Snellius-Descartes-féle törvény a két határfelületre vonatkozólag. Tegyük fel, hogy a fény nem-mágneses közegben terjed, ekkor μ1 = μ2 = μ3 = 1. A három nem-mágneses homogén közegre a karakterisztikus mátrixbeli q paraméter a 6.58. egyenlet alapján
|
|
(6.71) |
alakot ölti, ahol Z0 a vákuum hullámellenállása, valamint a felső index a polarizáció típusát (s és p), az alsó index (j = 1, 2, 3) a közeget azonosítja. Később látni fogjuk, hogy a lemez reflexiós és transzmissziós együtthatói visszavezethetők a határfelületeknek a Fresnel-féle egyenletekből számolható reflexiós és transzmissziós együtthatóira. Ezért célszerű ezeket a q paraméterekkel kifejezni. Egyszerű számolással beláthatjuk, hogy az i. és a j. közegek közötti felületek reflexiós tényezőit a
|
|
(6.72) |
összefüggések adják meg, ahol az s és a p indexet most elhagytuk, mert mindkét polarizációs fajtára azonos összefüggés vonatkozik. A transzmissziós együtthatók a
|
|
(6.73) |
formulákkal számolhatók ki a két polarizációs esetre vonatkozólag.
Homogén lemez reflexiós és transzmissziós tényezői
Az általános esetre vonatkozó reflexiós és transzmissziós együtthatókat már kiszámítottuk mind s-, mind p-polarizált hullám esetére. Most ezeket fogjuk a speciális esetre vonatkozólag alkalmazni, kihasználva, hogy a homogén közeg esetén a karakterisztikus mátrix a 6.59. analitikus formulával kiszámítható, így az általános 6.65. és 6.68. formulákban fellépő mátrix elemeket ismerjük, nevezetesen
|
|
(6.74) |
összefüggések adják meg ezeket, ahol a polarizációra vonatkozó s és p indexeket elhagytuk, mert mindkét esetre azonos formula érvényes, továbbá
|
|
(6.75) |
A 6.74 mátrix elemeket az s- illetve p-polarizált eseteket leíró 6.65. illetve 6.68. egyenletbe helyettesítve (qb = q1 és qt = q3 megfeleltetést használva), továbbá a határfelületekre vonatkozó reflexiós és transzmissziós együtthatókra vonatkozó 6.72. és 6.73. kifejezéseket figyelembe véve, az
| (6.76) |
egyenleteket kapjuk az amplitúdó reflexiós és transzmissziós tényezőkre, ahol a polarizációra vonatkozó indexet most is elhagytuk, mert a formula egyaránt érvényes s- és p-polarizált hullámra, csak nyilván az annak megfelelő tényezőt kell használni. Ezekből a fényteljesítményekre vonatkozó együtthatók a 6.66. egyenletek szerint
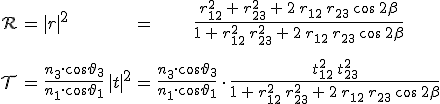 |
(6.77) |
összefüggésekkel számíthatók ki, ahol az utolsó alaknál feltételeztük, hogy az határfelületekhez tartozó együtthatók valósak, vagyis nem lép fel teljes visszaverődés, azaz a törési szög a 2. vagy 3. közegben nem válik komplex mennyiséggé. Közvetlen számolással most is megmutatható, hogy ![]() összefüggés érvényes, amely az energia megmaradását fejezi ki.
összefüggés érvényes, amely az energia megmaradását fejezi ki.
A 6.76. összefüggésekhez elemi úton is el lehet jutni. Viszonylag egyszerűen megmutatható, hogy a két határfelületen a lemezen belül többszörösen oda-visszaverődő, és a felületen átmenő hullámokat összeadjuk, akkor egy geometriai sorhoz jutunk. A geometriai sor összegképletét használva 6.76. szintén megkapható. Nyilván több réteg esetén ez a módszer egyre nehézkesebben használható, míg az itt leírt karakterisztikus mátrixszal a számolások egyszerűbben elvégezhetők. Ebből a megjegyzésből az is világos, hogy a kifejtett eljárás számot ad a lemezen belüli többszörös visszaverődések következtében létrejövő interferencia okozta jelenségekről is.