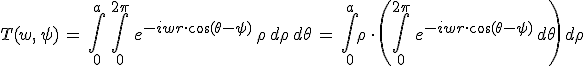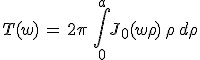Fraunhofer-elhajlás környíláson

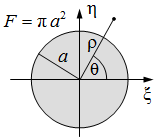
	10.11. ábra.  Kör alakú nyílás. A szürkével jelölt rész átlátszó.

Vizsgáljuk meg az alkalmazásokban gyakori, és ezért fontos esetet, mikor a fény egy kör alakú nyíláson hajlik el. Jelölje a a nyílás sugarát. A számolásnál a (ξ, η) és a (k_ξ, k_η) változók helyett célszerű áttérni a (ρ, θ) és a (w, ψ) polárkoordinátákra, melyeket a

      és        

      és     

összefüggésekkel vezetünk be. Ezekkel , és így a 10.47. integrált az

(10.53)

alakba írhatjuk. Amiből látható, hogy a T függvény valójában független a ψ szögtől, mert az exponensben lévő függvény θ szögnek periodikus függvénye, és az integrált egy teljes periódusra végezzük. Az integrál értéke nem függ a kezdőponttól, így a θ – ψ változó helyettesítéssel az állítás könnyen igazolható. Ennek megfelelően a 10.53. formulában ψ változót zérusnak tekinthetjük. Így, felhasználva a nullad-rendű Bessel-féle függvényre vonatkozó

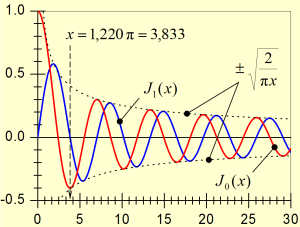
	10.12. ábra. A J0(x) (nullad-) és J1(x) (első-rendű) Bessel-függvények grafikonjai a [0, 30] intervallumon. Az első sötét gyűrű irányát a J1(x) első nullától különböző zérus helye határozza meg.

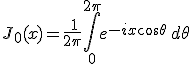
előállítást, a θ szög szerinti integrált visszavezethetjük a J₀(x) függvényre:

(10.54)

A 10.54. integrált pedig a J₁(x) (elsőrendű) Bessel-függvénnyel tudjuk kiszámolni, mivel a két Bessel-függvény között az

reláció áll fenn, így az integrandus primitív függvényét ismerjük, amiből az integrál könnyen kiszámítható. A két szóban forgó Bessel-függvény grafikonját a 10.12. ábra szemlélteti. Az elmondottak alapján

kifejezés adja meg a 10.47. integrált. Az, hogy ez a mennyiség csak w változó függvénye, az elhajlási kép hengerszimmetriáját fejezi ki. Ha α jelöli az (l, m) megfigyelési iránynak a beeső fény (l₀, m₀) irányával bezárt szögét, akkor alakba írhatjuk fel, amiből a 10.46. és a 10.48. összefüggéseket felhasználva, a környílás mögötti intenzitást az

(10.55)

formula adja meg. A 10.55. egyenletből számolt elhajlási kép a 10.13. ábra bal oldalán látható. A két elhajlás összehasonlítását az ábra jobb oldala mutatja, ahol az intenzitásokat az elhajlási szög szinuszának a függvényében ábrázoltuk. A kifejezésben megjelenő (2J₁(x)/x)² függvény viselkedés sokban hasonlít a résnél látott (sinx/x)² függvényére. Például az x = 0 helyen ez a függvény 0/0 típusú, továbbá a határértéke itt szintén 1. Ugyancsak az x = 0 helyen van a főmaximum, melyet mellékmaximumok követnek, ezek azonban gyorsabban csökkennek. Az ábráról láthatjuk, hogy a rés szélességével azonos átmérőjű környílás esetén a kioltási irányokhoz tartozó szögek ugyan kissé nagyobbak, azonban a mellékmaximumok kisebbek, és gyorsabban is csökkennek. Az első sötét gyűrűhöz tartozó irányt a J₁(x) első nullától különböző zérus helyéből számolhatjuk ki. A 10.12. ábráról leolvasva a zérushely értékét, azt kapjuk, hogy az első sötét gyűrűt megadó irányra az

(10.56)

összefüggés áll fenn.

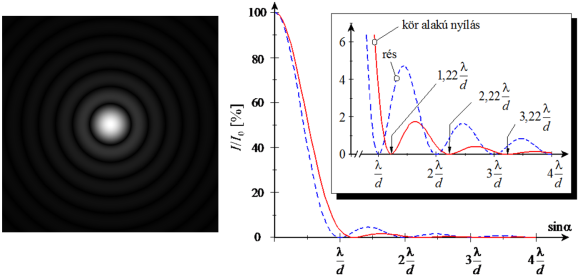10.13. ábra. Fraunhofer-féle elhajlási kép környílás esetén (balra). Az intenzitás függése az elhajlási szög szinuszától környílás illetve rés esetén azonos átmérő illetve szélesség esetén.