Síkhullámok

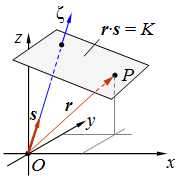
	2.1. ábra. A síkhullám képleténél alkalmazott je- lölések.

Jelölje az origóból a P pontba mutató helyvektort (2.1. ábra), és legyen egy tetszőleges, a gondolatmenetünk során rögzített, egységvektor , amely a térben egy irányt jelöl ki. Keressük a 2.7. skaláris hullámegyenlet

(2.8)

alakú megoldásainak általános alakját. A 2.8. típusú megoldásokat síkhullámnak nevezzük, mivel egy adott t időpontban az egyenlettel meghatározott síkokban V állandó. A síkot melyben V állandó hullámfelületnek, az ezekre merőleges s egységvektort hullámnormálisnak nevezzük. A megoldás legegyszerűbben egy olyan vonatkoztatási rendszerben kereshető meg, melynek a z tengelye az s vektorral párhuzamos. Jelölje a P pont koordinátáit ebben a vonatkoztatási rendszerben (ξ, η, ζ). Ebben a koordináta-rendszerben a definíció alapján s = (0, 0, 1), és ezért

.

(2.9)

 Ebből az összetett függvényre vonatkozó differenciálási szabályt használva

  ,        és   .

Amiből következik, hogy , ahol a zárójelben lévő összeg 1, hiszen s egységvektor. Ezért a hullámegyenlet a (ξ, η, ζ) koordinátákkal

(2.10)

alakot ölti. Ha bevezetjük az

és   a

(2.11a-b)

 új változókat, akkor ezekkel a ζ és t szerinti deriváltakat a

formulákkal számolhatjuk át. A második deriváltakat ugyanilyen módon kiszámolva és 2.10. egyenletbe helyettesítve, és a vegyes parciális deriválás sorrendjét felcserélve, a

formulát nyerjük. Amiből már látható, hogy az egyenlet általános megoldása

,

(2.12)

ahol  f  és g tetszőleges egyváltozós, kétszer differenciálható függvények. Visszatérve az eredeti változókra, azaz a 2.12. egyenletnél a 2.11. a-b és a 2.9. összefüggéseket felhasználva kapjuk, hogy

,

(2.13)

amely a keresett síkhullámra vonatkozó általános formula.

Könnyen belátható, hogy a 2.13. egyenletbeli  f  függvénnyel adott kifejezés egy +s irányba (másképpen mondva +ζ irányba) c sebességgel terjedő zavart ír le. Ugyanis, ha egy r₀ pontban és t₀ időpontban az f argumentuma K₀ = s·r₀ − c·t₀, és a zavar c sebességgel terjed, akkor az r₀ ponton átmenő s irányú egyenesen az r₀ ponttól éppen Δs = c·Δt távolságra lévő r = r₀ + Δs·s pontban a t = t₀ + Δt időben a függvény s·r − c·t argumentumának szintén K₀-lal kell megegyeznie. Ami valóban teljesül, mivel s·r − c·t = s·[r₀ + (c·Δt)·s] − c·(t₀ + Δt) = s·r₀ − c·t₀ = K₀. Vagyis 2.13. formula első tagja valóban egy s irányba c sebességgel terjedő zavart ír le. Teljesen hasonlóan látható be, hogy az összeg második tagja -s irányba c sebességgel terjedő zavart ad meg. Ismételten kiemeljük, hogy a 2.13. egyenlettel adott függvény az s irányra merőleges síkokban egy adott időpontban azonos értékeket vesz fel. Ami azt jelenti, hogy ezen egyenlettel leírt a hullámnak a hullámfrontjai az s irányra merőleges síkok.