A síkhullámok tulajdonságai

Mivel ε állandó, az  M-3 egyenletből és az 1.3. anyagegyenletből következik a feltétel. Vizsgáljuk meg, hogy ez a feltétel mit jelent a 3.4. egyenlettel meghatározott E vektor esetén. Jelöljük a Descartes-féle derékszögű koordinátákat az 1, 2 és 3 indexekkel (a szokásos x, y, z jelölés mellett ezt is fogjuk használni), és számoljuk ki E divergenciáját! Ha u = ct − s·r = ct − (s₁·x₁ + s₂·x₂ + s₃·x₃), akkor ∂/∂x_j = −s_j·d/du ( j = 1, 2, 3) és ∂/∂t = c·d/du, ezért

  .

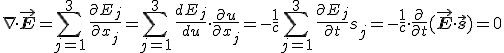Ebből következik, hogy az E·s időfüggetlen, azaz csak a helytől függ, amit E·s = E₀(r)·s alakba írhatunk fel, ahol E₀(r) egy statikus elektromos mező, amely nyilván nem hullámjelenséget ír le. Az optikában a fényhullámokkal foglalkozunk, így ezt a statikus mezőt az optikában zérusnak tekinthetjük, vagy a Maxwell-egyenletek lineáris volta miatt bármikor levonhatjuk a térerősségből. Ezen megjegyzések után mondhatjuk, hogy a tisztán hullámjelenséget leíró E térerősségre E·s = 0, ami azt jelenti, hogy E és s egymásra merőleges vektorok (). Az M-4 egyenletből és az 1.7. anyagegyenletből a feltételt kapjuk, amiből E-hez hasonlóan következik, hogy a H mágneses térerősség szintén merőleges az s vektorra ().

Mivel s a terjedési irányt jelöli ki, az eredményünket úgy is megfogalmazhatjuk, hogy mind az E elektromos, mind a H mágneses térerősség a terjedési irányra merőlegesen rezeg, ami azt jelenti, hogy a fény transzverzális hullám.

Ismét használva a 3.4. egyenletbeli E vektor esetén érvényes ∂/∂x_j = −s_j·d/du ( j = 1, 2, 3) és ∂/∂t = c·d/du deriváltakra vonatkozó szabályokat,

.

Ezt az M-2 egyenletbe helyettesítve, és az 1.7. anyagegyenletet felhasználva

egyenlethez jutunk, amely azt jelenti, hogy a zárójelben lévő kifejezés időben állandó. Ezt az integrálási állandót zérusnak választva

(3.5)

összefüggés adódik, ahol az ekvivalens átalakításoknál a c = c₀/n, a és az  relációkat használtuk fel, továbbá bevezettük az elektromos és a mágneses térerősségek nagyságainak a

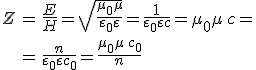(3.6)

hányadosát, a közeg hullámellenállását, vagy más néven hullámimpedanciáját, melynek SI egysége megegyezik az elektromos ellenállás egységével, vagyis 1 Ohm. A 3.5. egyenlet azt mutatja, hogy H mágneses térerősség az E elektromos térerősségre és az s terjedési irányra merőlegesen rezeg.

A 3.4. egyenlettel adott H vektoriális síkhullámot és az 1.3. anyagegyenletet az M-1 egyenletbe helyettesítve, az előző eljáráshoz teljesen hasonlóan megmutatható, hogy

,

(3.7)

amely közvetlenül 3.5. egyenletből is közvetlenül megkapható, ha az egyenletet jobbról vektoriálisan szorozzuk s vektorral, és a többszörös vektoriális szorzatot a rá vonatkozó azonossággal kifejtjük, majd kihasználjuk, hogy s az E-re merőleges egységvektor.

Összefoglalva, eredményünk azt mutatja, hogy a 3.4. egyenlettel leírt vektoriális síkhullámok csak akkor megoldásai a Maxwell-egyenleteknek, azaz fizikailag megengedett elektromágneses síkhullám, ha a 3.5. és 3.7. feltételek teljesülnek, mely szerint s, E és H jobbsodrású, egymásra páronként merőleges vektorrendszert alkotnak, és mivel s állandó vektor, E és H időben és térben azonos módon változnak.

A 3.5. (vagy a 3.7.) egyenletekből kiindulva már könnyen kiszámíthatjuk a homogén lineáris és izotrop közegben terjedő elektromágneses hullámra energiaviszonyait jellemző mennyiségeket. Az 1.24. egyenletbe helyettesítve az 1.3. és 1.7. anyagegyenleteket, az elektromágneses mező energiasűrűségére

(3.8)

adódik, ahol és . Az összeg első tagja az elektromos, míg a második tagja a mágneses tér energiasűrűségét adja meg. Mivel s vektor E vektorra merőleges egységvektor, a 3.5. egyenletből kifolyólag

,

(3.9)

amiből következik, hogy w_m = w_e, azaz a mágneses és az elektromos tér energiasűrűsége megegyezik, ezért

.

(3.10)

Az elektromágneses síkhullámban az energia a hullámfrontokkal azonos irányba áramlik, mivel a 3.5. (vagy a 3.7.) egyenletekből következőleg az

(3.11)

Poynting-vektor a s vektorral azonos irányú. A 3.10. és a hullámimpedancia definícióját felhasználva az

(3.12)

lényeges összefüggéshez jutunk, melyben - emlékeztetőül - w a mező energiasűrűsége és c a közegbeli fénysebesség. Mivel a fény intenzitása a fényáramlás energiasűrűségének (Poynting-vektor) nagyságának az időbeli átlagos értéke, az intenzitást az

(3.13)

formulából számíthatjuk ki, ahol  az energiasűrűség időbeli átlaga.

Vizsgáljuk meg, hogy az alkalmazásoknál fontos  monokromatikus hullámok esetén hogyan számítható ki az intenzitás. Egyszerűen megmutatható, hogy függvény egy periódusra vonatkozó átlaga A²/2, így egy monokromatikus hullám térerősségének egy periódusra vonatkozó átlaga  ahol A a térerősség valós és a komplex amplitúdója, φ a térerősség térfüggő fázisa. Így monokromatikus hullámok esetén a 3.10 és 3.13. összefüggésekből

.

(3.13a)

egyenletet kapjuk az intenzitásra.