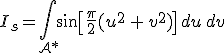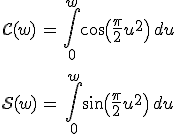Fresnel-féle elhajlás
 |
|
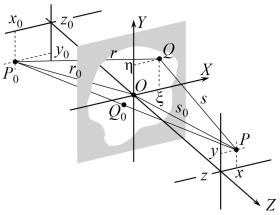
| 10.14. ábra. Jelölések Fresnel-féle elhajlás esetén. A fényforrás a P0 pontban van. Q0 jelöli a P0P szakasz az elhajlító ernyő síkjában lévő pontját. |
Fresnel-féle elhajlás esetén az f(ξ,η) függvény a 10.42. egyenlet szerinti másodrendű közelítésében fellépő ξ·η keresztszorzatot tartalmazó tag is megjelenik. Ez ugyan megfelelő koordinátatranszformációval eltüntethető, azonban ekkor még a legegyszerűbb esetekben is, például rés vagy él esetén a megjelenő integrálok határa változó lesz, amely nehezíti a formulák használatát. Ez a nehézség elkerülhető az említett egyszerű esetekre vonatkozólag, ha a 10.37. helyett az
|
|
(10.57) |
illetve a 10.40. közelítés helyett az
|
|
(10.58) |
összefüggéseket alkalmazzuk, melyek a vizsgált estekben az előzőekhez hasonlóan jó közelítésnek tekinthetők. A 10.57. és 10.58. közelítéseket az origóra (ξ = 0 és η = 0) alkalmazva
|
|
(10.59) |
összefüggéseket kapjuk a megfigyelési hely és a forrás origótól mért távolságaira. A 10.57. és 10.58. közelítésekben felbontva a zárójeleket, és a 10.59. egyenleteket is felhasználva
|
|
(10.60) |
adódik, amiből a 10.35. összefüggésből látható, hogy
|
|
(10.61) |
A 10.61. összefüggés előnye, hogy ebben már nem jelenik meg a ξ·η keresztszorzat, amely jelentősen könnyíti a 10.34. egyenletbeli integrál kiszámítását. Az Euler-formulát használva a térerősséget a
|
|
(10.62) |
alakba írhatjuk, ahol
|
|
(10.63) |
továbbá
|
|
(10.64) |
ahol 10.34. egyenletben a nevezőben lévő s0 és s távolságokat a fényforrás illetve a megfigyelési hely síkjainak a nyílás síkjától mért d0 = –z0 és d = z távolságaival közelítettük.
A 10.63. integrálok kiszámolását érdemes a P ponttól függő "lokális" koordináta-rendszerben elvégezni. Az origó helyét az elhajlító nyílás síkjában szabadon megválaszthatjuk. Ha az origót az ernyőnek abba - a 10.14. ábrán Q0-lal jelölt - a pontjába helyezzük, ahol a P0P szakasz kimetszi az ernyőt, akkor a 10.61. összefüggésben a lineáris rész eltűnik. Jelölje az eredeti vonatkoztatási rendszert K, a Q0 pontba eltolt origójú vonatkoztatási rendszert K'. Ebben a pontok koordinátáit szintén vessző fogja jelölni, például Q = (ξ', η'). Érdemes megjegyezni, hogy K-ban levezetett (például a fenti) összefüggések K' is érvényben maradnak, csak a koordinátáknál a K'-beli koordinátákat (azaz vesszővel jelölteket) kell használni. Az egyszerűség kedvéért, ha a két koordináta-rendszerben a mennyiségek azonosak, vagy a szövegből egyértelműen kiderül, hogy melyik koordináta-rendszerről van szó, a vessző jelölést elhagyjuk.
Egyszerű számolással belátható, hogy a Q0 = (ξ0, η0) pontot az
|
|
(10.65) |
egyenletek adják meg. Ezek az egyenletek K'-ben is érvényesek (a vesszős jelöléssel). Mivel K'-ben Q0 az origó, azaz Q0 = (0, 0), így a 10.65. egyenletek első törtjeinek számlálója K'-ben zérus, amiből K'-ben ![]() és
és ![]() relációk állnak fenn, amiből következik a bevezetőben már említett tény, hogy 10.61. egyenletben a lineáris rész eltűnik, azaz másodrendű közelítésben f(ξ, η) a K' koordináta-rendszerben csak tisztán négyzetes tagokat tartalmaz. Az egyenes vonalú terjedésnek megfelelő, vagyis a geometriai optikai értelemben, megvilágított tartomány meghatározásánál hasznos a z síkbeli P pontnak a helyének a megadása a Q0 pont segítségével. A 10.65. egyenletekből egyszerű számolással az
relációk állnak fenn, amiből következik a bevezetőben már említett tény, hogy 10.61. egyenletben a lineáris rész eltűnik, azaz másodrendű közelítésben f(ξ, η) a K' koordináta-rendszerben csak tisztán négyzetes tagokat tartalmaz. Az egyenes vonalú terjedésnek megfelelő, vagyis a geometriai optikai értelemben, megvilágított tartomány meghatározásánál hasznos a z síkbeli P pontnak a helyének a megadása a Q0 pont segítségével. A 10.65. egyenletekből egyszerű számolással az
|
|
(10.66) |
kifejezések adódnak. A z síkban lévő megfigyelési ernyőn a geometriai árnyék határát ezen összefüggések a segítségével könnyen meg tudjuk adni: ha a Q0 = (ξ0, η0) pontot körbevisszük a nyílás peremén, a P pont a geometriai árnyék határát jelöli ki az ernyőn.
Az előkészületek után már könnyen fel tudjuk írni a 10.62. egyenletbeli mennyiségeket K'-ben is. Felhasználva, hogy K'-ben ![]() és
és ![]() , a 10.64. egyenlettel meghatározott komplex amplitúdóra a
, a 10.64. egyenlettel meghatározott komplex amplitúdóra a
|
|
(10.67) |
összefüggést kapjuk, ahol ![]() a P0P szakasz hossza és a D mennyiséget az
a P0P szakasz hossza és a D mennyiséget az
|
|
(10.68) |
egyenlet definiálja. Az integrálban a szögfüggvények argumentumában fellépő kifejezést a
|
|
(10.69) |
alakban adhatjuk meg a K' koordináta-rendszerben. Ha az integrálban végrehajtjuk az
|
|
(10.70) |
változó helyettesítést, akkor az 10.63. integrálokra a
|
|
(10.71) |
kifejezések adódnak, ahol a ![]() a nyílás pontjait jelöli az
a nyílás pontjait jelöli az ![]() változókkal kifejezve, valamint az Ic és Is az integrálok tömör jelölésére szolgálnak. Mindezek alapján a P pontbeli térerősséget
változókkal kifejezve, valamint az Ic és Is az integrálok tömör jelölésére szolgálnak. Mindezek alapján a P pontbeli térerősséget
|
|
(10.72) |
alakban kaptuk meg, amelyből a szorzó tényezők fizikai jelentése jól kivehető. Az első tényező a nyílás hiányában (zavartalanul) terjedő hullámot írja le. Így a második tényező hordozza az elhajlás következtében megjelenő eltérést. Az
|
|
(10.73) |
 |
|
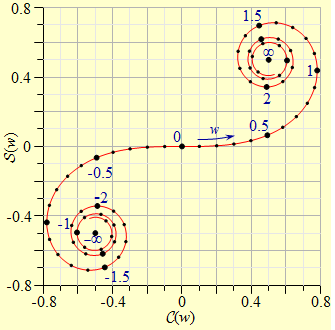
| 10.15. ábra. A Fresnel-féle integrálokat grafikusan szemléltető Cornu-féle spirál. |
integrálok kiszámítását gyakran visszavezethetjük az ún. Fresnel-féle integrálokra, melyeket a
|
|
(10.74) |
formulák definiálnak, és grafikusan a 10.15. ábrán látható Cornu-spirállal szokás szemléltetni. Síkbeli koordináta-rendszerben adott w esetén ábrázolva a ![]() pontot, a w paramétert változtatva az (1/2, 1/2) és a (-1/2, -1/2) pontokra "rátekeredő" spirált kapjuk. A görbe mellett bizonyos pontokban feltüntettük a w paraméter értékét. A definíciókból következik, és az ábrából is látható, hogy a Fresnel-integrálok a w paraméter páratlan függvényei. A w = ∞ esetén
pontot, a w paramétert változtatva az (1/2, 1/2) és a (-1/2, -1/2) pontokra "rátekeredő" spirált kapjuk. A görbe mellett bizonyos pontokban feltüntettük a w paraméter értékét. A definíciókból következik, és az ábrából is látható, hogy a Fresnel-integrálok a w paraméter páratlan függvényei. A w = ∞ esetén
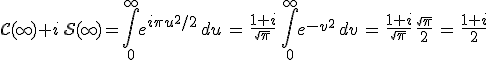 ,
,
amiből következik, hogy ![]() . A Fresnel-integrálokat sok matematikai program már beépített függvényként tartalmaz. Numerikusan, kis argumentumokra a szögfüggvények hatványsoraiból tagonkénti integrálással nyert sorokból, míg nagy argumentumokra parciális integrálásokkal kapható aszimptotikus sorfejtéssel számíthatjuk ki [1].
. A Fresnel-integrálokat sok matematikai program már beépített függvényként tartalmaz. Numerikusan, kis argumentumokra a szögfüggvények hatványsoraiból tagonkénti integrálással nyert sorokból, míg nagy argumentumokra parciális integrálásokkal kapható aszimptotikus sorfejtéssel számíthatjuk ki [1].
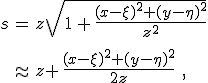
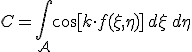 és
és 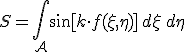 ,
,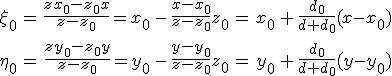
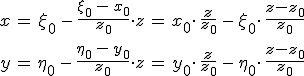
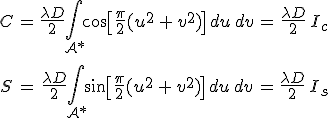
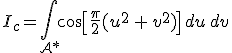 és
és