Maxwell-féle egyenletek

Egy vezetőben folyó áram (vagyis a mozgó töltések) a vezető körül mágneses teret hoz létre. Időfüggetlen esetben a kialakuló mágneses tér erősségét az Ampere-féle gerjesztési törvény adja meg, amely szerint az adott felületen átfolyó áramerősség egyenlő a mágneses térerősség cirkulációjával, azaz a felületet határoló görbére vonatkozó vonalintegráljával. A időfüggő esetben az áramerősséghez még hozzá kell adni a - Maxwell által bevezetett - eltolási áramot, melynek a sűrűségét az elektromos eltolás idő szerinti deriváltjával egyezik meg. Az eltolási árammal kiegészített gerjesztési törvény matematikai megfogalmazása az első integrális Maxwell-egyenlet, amely szerint egy F felületre és az azt határoló C görbére

,

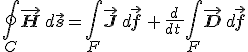(IM-1)

ahol H a mágneses térerősség, J a makroszkopikus áramsűrűség és D az elektromos eltolás. A második felületi integrálnál az integrálás és a deriválás sorrendje felcserélve, és a baloldali vonalintegrált a Stokes-féle tétellel átírva H rotációjának felületi integráljára, továbbá kihasználva, hogy a I-1 egyenlet tetszőleges F felületre érvényes, kapjuk az első (differenciális) Maxwell-egyenletet:

.

(M-1)

A ∂D/∂t mennyiség a - Maxwell által bevezetett - eltolási áramnak a sűrűsége. Látni fogjuk, hogy a Maxwell-féle egyenletekből következik a töltés megmaradást kifejező kontinuitási egyenlet. Az eltolási áram figyelembe vétele nélkül, - csupán az Ampere-féle gerjesztési törvényt használva - a kontinuitási egyenletnek ellentmondó összefüggés származna.

Faraday kísérletei óta ismert, hogy ha egy zárt vezetőkör felületén a mágneses tér fluxusa változik, akkor a vezetőben áram indul meg. Ez a változó mágneses tér által indukált elektromos tér jelenlétére utal, hiszen a töltéseket a fellépő elektromos erő mozgatja. Az indukciós törvény matematikai megfogalmazása a második integrális Maxwell-egyenlet, amely szerint egy F felületre és az azt határoló C görbére

,

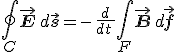(IM-2)

 ahol E az elektromos térerősség és B a mágneses indukció. A baloldali vonalintegrált a Stokes-féle tétellel átírva E rotációjának felületi integráljára, a jobb oldalon az integrálás és a deriválás sorrendjét felcserélve, továbbá kihasználva, hogy a IM-2 egyenlet tetszőleges F felületre érvényes, a

(M-2)

összefüggést kapjuk, amely a második (differenciális) Maxwell-féle egyenletet.

Az elektromos tér forrásai az elektromos töltések, amely szemléletesen abban nyilvánul meg, hogy az erővonalak vagy egy töltésből indulnak ki és egy másik töltésben végződnek, vagy - változó mágneses tér által indukált elektromos mező esetén - zárt görbék. Ennek megfelelően egy zárt felületre vonatkozó elektromos fluxust a felület által körbevett térrészben lévő töltés határozza meg. Ezt - a tapasztalatból levont - szabályt fogalmazza meg az elektromos Gauss-törvényként ismert összefüggés, amely szerint egy tetszőleges V térfogatra és annak F felületre

,

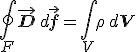(IM-3)

ahol D az elektromos eltolás és ρ a makroszkopikus elektromos töltéssűrűség. Az I-3 formula a harmadik integrális Maxwell-egyenlet. A baloldali zárt felületre vonatkozó integrált a (matematikai) Gauss-féle tétellel átírva D divergenciájának V-re vonatkozó térfogati integráljára, és mivel az I-3 egyenlet tetszőleges V térfogatra érvényes, a

(M-3)

összefüggés áll fenn minden pontban, amely a harmadik (differenciális) Maxwell-féle egyenletet.

A tapasztalat azt mutatja, hogy az elektromos töltéstől eltérően különálló egynemű mágneses töltések, más néven mágneses monopólusok nem léteznek. A legegyszerűbb elemi mágneses töltésrendszer a dipólus, melyeket atomi vagy molekuláris köráramok hoznak létre. Ennek megfelelően egy zárt felületre vonatkozó mágneses indukció fluxusa zérus a felületen, mivel az erővonalak zártak, így vagy teljesen a térfogaton belül haladnak, vagy ha kilépnek, akkor vissza is kell lépniük. Ezt a tapasztalatból levont következtetést önti matematikai formába az elektromos Gauss-törvény, amely szerint egy tetszőleges V térfogatra és annak F felületre

,

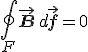(IM-4)

ahol B a mágneses indukció. Az IM-4 formula a negyedik integrális Maxwell-egyenlet. A harmadik Maxwell-egyenlethez hasonlóan, a Gauss-tétel felhasználva, a

(M-4)

formulához juthatunk, amely a negyedik - differenciális - Maxwell-féle egyenletet. A mágneses monopólusok hiányával magyarázhatjuk az első és második Maxwell-egyenletek közötti különbséget, nevezetesen a második Maxwell-egyenletbeli mágneses áramsűrűség hiányát.