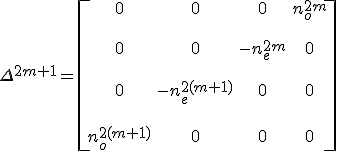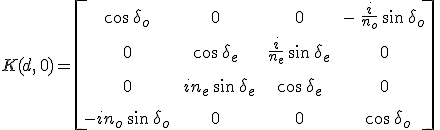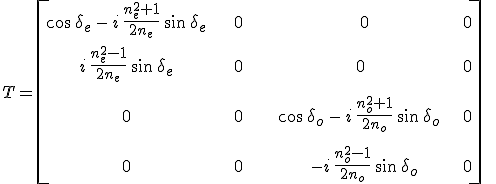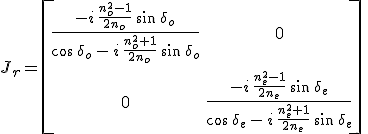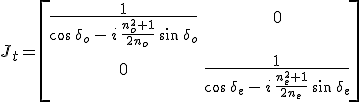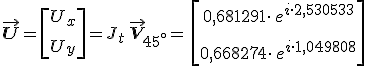Példa: hullámlemez
A fejezetben bemutatott eljárással vizsgáljunk meg példaként gyakorlati szempontból nagy jelentőséggel bíró hullámlemez hatását. A hullámlemezek általában egytengelyű kristályból készített olyan sík-párhuzamos lemezek, amelynél az optikai tengely a lemez síkjába esik. Szinte minden optikai könyvben és bevezető optika előadásokban is megemlítik, hogy egy ilyen lemez a rá merőlegesen beeső monokromatikus síkhullám optikai tengely irányába és az erre merőleges térerősség komponensek között
|
|
(12.55) |
fáziskülönbséget hoz létre, ahol 
és 
az egytengelyű kristály fősebességeihez tartozó törésmutatók, d a lemez vastagsága és λ a vákuumbeli hullámhossz. Azonban az már kevésbé ismert tény, hogy ez a szemléletből adódó megállapítás nem teljesen pontos! Mégpedig azért, mert a gondolatmenet során elhanyagolják a lemez alsó és felső felületén létrejövő hullámfrontosztásokat, és az ennek következtében kialakuló interferenciát. A térerősség két komponensének irányában az és közötti kicsi különbség miatt a két komponensre vonatkozó reflexiós és transzmissziós tényezők is különbözőek egy kicsit, ezért az interferencia okozta fázistolások is kissé eltérőek. A szemléletes kép ezeket a hatásokat elhanyagolja. A szemlélet alapján azt várjuk, hogy ha a beeső fény lineárisan poláros és a rezgési síkja az optikai tengellyel 45º-os szöget zár be, valamint a lemez vastagságát a
|
|
(12.56) |
összefüggés szerint választjuk meg (m = 0, 1, 2, …), akkor a lemezt cirkulárisan poláros fény hagyja el, mivel a kilépő fény két egymásra merőleges komponensének amplitúdója azonos és a közöttük a 12.55. egyenletből kifolyólag 
fáziskülönbség van, ahol m egész szám. Látni fogjuk, hogy ez csak közelítőleg teljesül. Az eltérést pedig a nevezett hatások elhanyagolása okozzák.
A hullámlemez átviteli mátrixa
Vizsgáljuk meg a problémát a bemutatott Berreman-féle eljárást használva! Mivel a hullám merőlegesen esik be, a beesési sík nem definiált, így az s- és p komponensek nem értelmezhetők. A beesési sík hiányába nyilván a koordináta-rendszert más szempont alapján kell kijelölni. Válasszuk meg a vonatkoztatási rendszert úgy, hogy az optikai tengely az y tengely irányába mutasson. Ehhez az orientációhoz a 
, 
Euler-szögek tartoznak. A harmadik Euler-szög határozatlan, mivel a kristály egytengelyű. A 12.21. egyenletek alapján nem mágneses anyagra (μ = 1) a dielektromos tenzort az
|
|
(12.57) |
mátrix reprezentálja a választott koordináta-rendszerben. Az s és p jelölés a ferde beeséshez van szabva. A formalizmus azonban változtatás nélkül alkalmazható az s ↔ y és a p ↔ x megfeleltetéssel. Vagyis a formalizmusban az s-komponensnek az optikai tengely (y tengely) irányába eső komponens, a p-komponensnek pedig az optikai tengelyre merőleges (x tengely) irányába eső komponens felel meg. Merőleges beesés miatt
|
|
(12.58) |
.A paramétereket a 12.30. egyenletekbe behelyettesítve a
|
|
(12.59) |
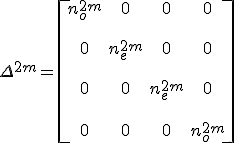
formulát kapjuk a Berreman-mátrixra. Ebből Δ páros és páratlan hatványaira az
|
|
(12.60) |
, 
összefüggések nyerhetők (m = 0, 1, 2, …). Ezeket felhasználva a 12.36. egyenlethez teljesen hasonló módon a
|
|
(12.61) |
kifejezés kapható lemez karakterisztikus mátrixára, ahol
|
|
(12.62) |
és 
a két törésmutatóhoz és d vastagsághoz tartozó fázistolás. A lemez alatti és feletti közeg törésmutatóját egységnyinek véve a 12.44. egyenletbe helyettesítve a
|
|
(12.63) |
adódik az átviteli mátrixra. Amiből a 12.50. összefüggések alapján a
|
|
(12.64) |
egyenletet kapjuk a visszaverődést leíró Jones-mátrixra. Hasonlóan a 12.54. egyenletbe helyettesítve a 12.63. átviteli mátrixot a
|
|
(12.65) |
kifejezést kapjuk a transzmisszióra vonatkozó Jones-mátrixra. Látható, hogy mindkét Jones-mátrix diagonális, ami azt jelenti, hogy a térerősség x és y komponense egymástól függetlenül terjed.
Példaként vizsgáljunk meg egy kalcitból készült λ/4-es lemezt. A kalcitnak λ = 589 nm hullámhosszon 
és 
a két törésmutató értéke. A 
, így a kalcit negatív egytengelyű kristály. A 
miatt az x irányú (főmetszetre merőleges ordinárius) komponens kisebb sebességgel terjed, mint az y irányú (főmetszetbe rezgő extraordinárius) komponens. Így a kalcitból készült λ/4-es lemez gyors illetve lassú tengelye az optikai tengelyre merőleges illetve vele párhuzamos, esetünkben az x illetve az y tengely irányba mutat. Ha a beeső fény β = 45º-os szögben lineárisan poláros, akkor a normált Jones-vektora a 4.1. táblázat szerint
|
|
(12.66) |
.A lemez vastagságát válasszuk 12.56. egyenlet alapján, az egyszerűség kedvéért az m = 0 esetnek megfelelően. A törésmutatók és a hullámhossz értékeit felhasználva d = 856,603 nm a lemez vastagsága. A lemezből kilépő fény Jones-vektorára
|
|
(12.67) |
vektort kapjuk, ahol Jt a 12.65. egyenletbeli Jones-mátrix. Ebből az y és x irányú komponens amplitúdóinak arányára és fáziskülönbségére
|
|
(12.68) |
és 
értékek adódnak. Ez szemmel láthatólag eltér a szemlélet alapján várt körben poláros eredménytől, melyhez az 
és a 
feltételek szükségesek. Vagyis a lemezből kilépő fény ellipszisben poláros lesz, - bár az eltérés kicsiny volta miatt - a polarizációs állapot közel esik a cirkulárisan poláros állapothoz.
Amint azt már említettük a különbséget a lemez két határfelületén bekövetkező egymást követő hullámfrontosztások, és az ennek következtében kialakuló interferencia elhanyagolása okozza. A lassú és gyors tengelyek irányába eső komponensekre - a nekik megfelelő törésmutatókkal - a Fresnel-formulákból a reflexiós és transzmissziós tényezőket kiszámolva, és síkpárhuzamos lemezen való soksugaras interferenciánál látott eljárást követve a fentivel azonos eredményt kapunk. Ennek belátását gyakorlásképpen az olvasóra bízzuk. A szemléletes képnél elhanyagolt jelenségek okozta eltérést kiküszöbölhetjük a lemez vastagságának kicsiny változtatásával és a beeső fény rezgési síkjának kicsi elforgatásával. Például, amennyiben 45º helyett a rezgési síkot a β' = 46,967º-os szögben állítjuk be, továbbá a lemezvastagságát d' = 1,024667·d = 877,732494 nm-re növeljük, akkor a kilépő fény már körben poláros lesz.
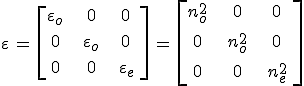
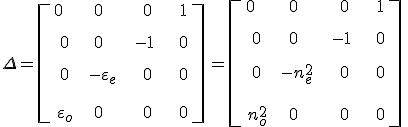