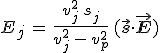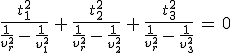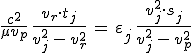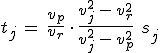Fresnel-féle sebességi egyenletek

Az elektromos eltolás vektort kifejezhetjük az ε (relatív) dielektromos tenzor segítségével az 1.3. anyagegyenlettel adott formában, továbbá a Maxwell-féle egyenletekből beláttuk, hogy az eltolás és a térerősség között fennáll a 11.13. egyenlet. Ezek alapján az

(11.30)

összefüggés teljesül. Ezt dielektromos főtengelyrendszerben koordinátákkal felírva és rendezve az

(11.31)

egyenletekhez jutunk , amely egy homogén és lineáris egyenletrendszer a térerősség E_j komponenseire. Ha jobb oldalon lévő törtet a értékkel bővítjük, akkor az

(11.32)

összefüggéseket kapjuk, ahol a fázissebesség és

(11.33)

a ε_j fődilektromos állandókból számolt ún. fősebességek . A 11.32. egyenletet a j = 1, 2, 3 indexekre s_j-vel szorozva, és az így nyert három egyenletet összeadva

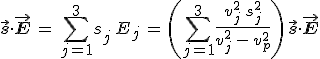
adódik. Amiből látható, hogy a zárójelben lévő összeg egységnyi. Így kihasználva, hogy s egységvektor, fennáll a

reláció. Ezt zérusra rendezve és a feltételt kihasználva az

(11.34)

összefüggést kapjuk, amely a Fresnel-féle sebességi egyenlet, vagy a Fresnel-féle normális egyenlet néven ismert. A 11.34. egyenletet megkaphattuk volna a 11.32. homogén és lineáris egyenletrendszer determinánsának a nulla voltából is, amely a triviálistól különböző megoldás létezésének a feltétele.

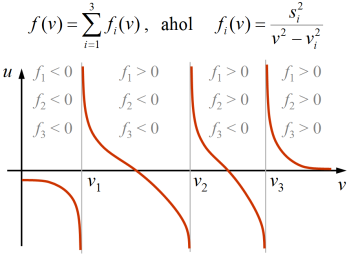	11.3. ábra. A Fresnel-féle sebességi egyenlet (11.34) bal oldalán álló u = f(v) függvény grafikonja. A fősebességeket a nagyságuk szerinti sorrendben indexeltük.

A kristályban terjedő s egységvektorral adott irányhoz tartozó v_p fázissebességet a 11.34. sebességi egyenletek gyöke szolgáltatja. Könnyen belátható, hogy pozitív értékeket tekintve általában két gyök van. Indexeljük a fősebességeket nagyság szerinti sorrendben, és jelölje a 11.34. egyenlet bal oldalán lévő összeg tagjait f₁, f₂ és f₃. Az f_i tagnak v_i helyen (i = 1, 2, 3) pólusa van , és v_i előtt negatív, utána pozitív. Így v₁ előtt az összeg negatív, majd v₁ értéket éppen átlépve - az első tag miatt - biztosan pozitív lesz. Viszont közvetlenül v₂ előtt - a középső tag miatt - biztosan megint negatív. Ezért az f(v) függvény folytonossága miatt a v₁ és v₂ között biztosan van  zérushely, ahol az előjelváltás bekövetkezik. Mivel az összegben az egyes tagok monoton módon változnak, csak egy zérushely van ezen az intervallumon. Teljesen hasonlóan magyarázható a v₂ és v₃ közötti gyök megléte.

Mivel egy adott s egységvektorral megadott terjedési irányhoz a Fresnel-féle sebességi egyenletnek általában két gyöke van, a kristályban egy adott irányhoz két v_p fázissebesség tartozik. Az adott fázissebességhez tartozó térerősséget a 11.32. homogén lineáris egyenlet határozza meg. Mivel a homogén egyenlet megoldásának állandószorosa szintén megoldás, így a 11.32 egyenlet csak az  arányokat határozza meg. Ugyancsak a 11.32 egyenlet alapján ezek az arányok valósak, így a térerősség lineárisan poláros rezgést végez. A 11.18. egyenlet miatt arányok szintén valósak, ami azt jelenti, hogy a D elektromos eltolás is lineárisan poláros. Hamarosan meg fogjuk mutatni, hogy a két fázissebességhez tartozó polarizációs irány egymásra merőleges.

A dualitás-szabályt a 11.32. egyenletre alkalmazva kapjuk a

(11.35)

duális egyenletet. Ebből közvetlenül, vagy még egyszerűbben a 11.34. összefüggésre a dualitás-szabály alkalmazva kapható a

(11.36)

a sugársebességre vonatkozó Fresnel-féle sebességi egyenletet, vagy a Fresnel-féle sugárirány egyenletet, amelyből az adott t sugárirányhoz tartozó két sugársebesség számítható ki.

A sugárirány és a hullámnormális egymástól nem független. Az egyik már meghatározza a másikat. A közöttük lévő kapcsolat felderítése céljából tekintsük a 11.2. ábrát, melyről könnyen látható, hogy   és  . A 11.13. és az utóbbi két egyenlet felhasználva

összefüggést adódik. Az    és a    formulákat az előzőbe helyettesítve

(11.37)

képletet nyerjük. A 11.32. egyenletet ε₀·ε_j értékkel szorozva és a 11.8, a 11.35. és 11.37. egyenleteket összevetve az

(11.38)

relációkat kapjuk. A 11.33. egyenletből következő összefüggést behelyettesítve és rendezve az

(11.39)

formulák adódnak . Ebből már egyszerűen származtathatók a

(11.40)

egyenletek. A indexekre a 11.40. egyenletet négyzetre emelve, továbbá kihasználva a t és s vektorok egységnyi hosszát és a összefüggést a

(11.41)

formulát kapjuk. Ebből a relációból következik, hogy

,

(11.42)

ahol az első egyenlőség a definíció, míg a második már a 11.41 relációból adódik. Az egyenletből látható, hogy . A 11.42. egyenlettel definiált mennyiséget felhasználva a 11.39. egyenlet a

(11.43)

alakba írható át. Mivel általában egy bizonyos s hullámnormálishoz két v_p fázissebesség tartozik, így egy ehhez a hullámnormálishoz szintén két t sugárirány tartozik. Kéttengelyű kristályokban van két olyan szinguláris irány, amelyre 11.43. egyenletben a zárójelbeli tört nevezője nullává válik. Megmutatható, hogy a szinguláris s irányhoz végtelen sok t sugárirány tartozik, melyek s körül egy kúppaláston helyezkednek el. Hasonlóan kéttengelyű kristályokban van két szinguláris t sugárirány, melyhez szintén végtelen sok t körüli kúppaláston lévő s hullámnormális tartozik. Ezek az érdekes szinguláris irányokkal kapcsolatos a belső és külső kúpos törés jelensége [1], melyet a Fresnel-féle elmélet alapján W. R. Hamilton jósolt meg és kísérletileg H. Lloyd mutatott ki először.