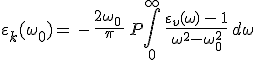Diszperziós relációk
Kramers-Kronig-integrálok
A 8.5. egyenlettel definiált komplex szuszceptibilitásnak, és így a belőle származtatott komplex dielektromos állandónak van egy különösen érdekes tulajdonsága: hamarosan látni fogjuk, hogy a valós és a képzetes részük nem függetlenek egymástól. Valójában elegendő az egyiket megadni, a másikat ez már meghatározza.
A kauzalitás 8.2. feltétele miatt a 8.5. egyenletbeli integrálnál az integrandus zérus negatív t értékekre, ezért
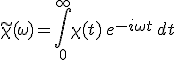 . . |
(8.22) |
Ez a függvény a valós számegyenesen van értelmezve, de az 8.22. integrál alapján kiterjeszthető a komplex síkra. Ha ![]() , akkor
, akkor
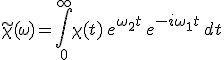 , , |
(8.23) |
amelyből következik, hogy az ω2 ≤ 0 alsó komplex félsíkon holomorf (vagy másképp mondva analitikus, azaz az ω a komplex változó szerint differenciálható). Legyen ω0 tetszőleges valós körfrekvencia, és tekintsük a
| (8.24) |
 |
|
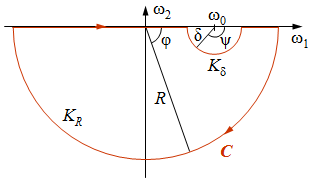
| 8.2. ábra. Az integrálási útvonal. Az integrandus valós tengelyen lévő pólusát egy δ sugarú félköríven kerüljük ki. |
függvényt. Az elmondottak szerint h függvény is holomorf az alsó komplex félsíkon kivéve a valós tengelyen fekvő ω0 pontot. Ezért a komplex függvénytan Cauchy-féle integráltétele szerint h bármely az előbbi tartományban fekvő zárt görbére vonatkozó integrálja zérus, így nulla a 8.2. ábrán látható C görbére vonatkozólag is, azaz
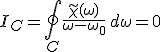 . . |
(8.25) |
Az integrálási útvonal a valós tengelyen lévő (–R, ω0 – δ) és a (ω0 + δ, R) egyenes szakaszokból és egy δ > 0 és egy R > 0 sugarú Kδ és KR félkörívekből áll, a görbe körbejárási irányát a nyíl mutatja. Az integrált felbonthatjuk ezekre a szakaszokra, így
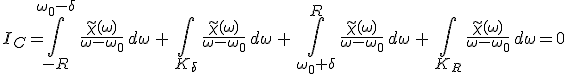 .
.
A félköríveket a ψ és a φ szögekkel paraméterezve
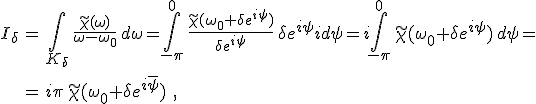
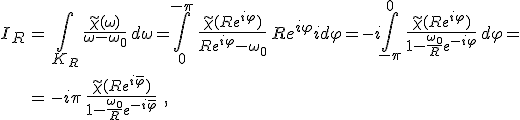
ahol ![]() és
és ![]() és a két integrál utolsó átalakításánál az integrálszámítás (folytonos függvényekre) vonatkozó középértéktételét használtuk fel. Vizsgáljuk meg, hogy miként viselkednek a félkörívekre vonatkozó integrálok δ → +0 illetve R → ∞ esetén. A
és a két integrál utolsó átalakításánál az integrálszámítás (folytonos függvényekre) vonatkozó középértéktételét használtuk fel. Vizsgáljuk meg, hogy miként viselkednek a félkörívekre vonatkozó integrálok δ → +0 illetve R → ∞ esetén. A ![]() függvény folytonossága miatt
függvény folytonossága miatt
![]()
áll fenn. A 8.23. egyenlet következtében, mivel ![]() az alsó komplex félsíkon van, így
az alsó komplex félsíkon van, így ![]() ha R → ∞, valamint
ha R → ∞, valamint ![]() amennyiben R → ∞. Ezeket figyelembe véve
amennyiben R → ∞. Ezeket figyelembe véve
![]() .
.
A fentieket mind figyelembe véve 8.25. egyenletből
|
|
(8.26) |
az összefüggés következik, ahol a P szimbólum az integráljel előtt a Cauchy-féle főértékre utal. Ha
![]()
előállítást behelyettesítjük és az egyenlet két oldalán a valós és a képzetes részeket egyenlővé tesszük, akkor
|
|
(8.27) |
úgy nevezett diszperziós relációkhoz, vagy más néven a Kramers-Kronig-integrálokhoz jutunk. Ha a komplex dielektromos állandót is a már látott
![]()
alakba írjuk fel, akkor a ![]() összefüggés miatt
összefüggés miatt ![]() és
és ![]() áll fenn, és így a 8.27. Kramers-Kronig-integrálok integráloknak a dielektromos állandóra vonatkozó alakja
áll fenn, és így a 8.27. Kramers-Kronig-integrálok integráloknak a dielektromos állandóra vonatkozó alakja
|
|
(8.28) |
Közvetlen számolással ellenőrizhető, hogy a Lorentz-féle modellből adódó 8.10. függvények teljesítik ezeket az összefüggéseket, azaz a a Lorentz-féle modell Kramers-Kronig konzisztens. Kihasználva, hogy ![]() páros,
páros, ![]() páratlan függvények, azaz
páratlan függvények, azaz ![]() és
és ![]() tulajdonságok állnak fenn, a 8.28. integrálok könnyen átírhatók az
tulajdonságok állnak fenn, a 8.28. integrálok könnyen átírhatók az
|
|
(8.29) |
alakba, amelyben már csak a fizikai jelentéssel rendelkező nem negatív körfrekvenciákra kell integrálni.
A 8.28. vagy a 8.29. Kramers-Kronig-integrálok a dielektromos állandóra vonatkoznak. A levezetésnél előírt feltételeket azonban gyakran nem csak ![]() , hanem az
, hanem az ![]() komplex törésmutató is teljesíti. Ezért, ha
komplex törésmutató is teljesíti. Ezért, ha ![]() analitikus az alsó komplex félsíkon és ezen a tartományon zérushoz tart a végtelenben (
analitikus az alsó komplex félsíkon és ezen a tartományon zérushoz tart a végtelenben (![]() , ha
, ha ![]() és
és ![]() ), akkor n és κ szintén Kramers-Kronig konzisztensek, azaz teljesítik a Kramers-Kronig- integrálokat.
), akkor n és κ szintén Kramers-Kronig konzisztensek, azaz teljesítik a Kramers-Kronig- integrálokat.
A szakirodalomban szintén gyakran használják a monokromatikus hullámok időfüggésére az ![]() kifejezést, az általunk használt
kifejezést, az általunk használt ![]() helyett. Ekkor a dielektromos állandót az
helyett. Ekkor a dielektromos állandót az ![]() , a törésmutatót pedig és az
, a törésmutatót pedig és az ![]() alakban szokták felírni, és a Fourier-traszformáció formulái is az exponens előjelében különböznek. Ilyenkor a
alakban szokták felírni, és a Fourier-traszformáció formulái is az exponens előjelében különböznek. Ilyenkor a ![]() a felső komplex félsíkon analitikus, és mivel az integrálási útvonalnak a holomorfia tartományban kell lennie, a 8.2. ábrán látható görbének valós tengelyre vonatkozó tükörképét kell a levezetésnél használni.
a felső komplex félsíkon analitikus, és mivel az integrálási útvonalnak a holomorfia tartományban kell lennie, a 8.2. ábrán látható görbének valós tengelyre vonatkozó tükörképét kell a levezetésnél használni.
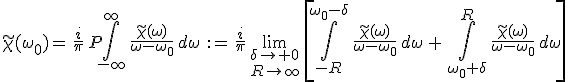
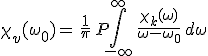 és
és 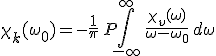
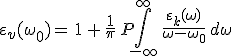 és
és 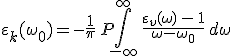 .
. 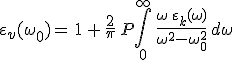 és
és