Kéttengelyű kristályok

Mutassanak a koordináta-rendszerünk tengelyei a dielektromos főtengelyek irányába úgy, hogy az egyes tengelyekre vonatkozó fődielektromos állandók nagyság szerint rendezve legyenek. Így fennáll az reláció, amiből a fősebességekre a

(11.74)

viszony teljesül. Az egységvektor által megadott irányhoz tartozó fázissebességet a 11.64. egyenlet gyökei adják meg. Kéttengelyű kristályok esetén a viszonyok összetettebbek az egytengelyűhöz képest, ezért célszerű kezdetben a vizsgálatot a koordináta tengelyek által kifeszített síkokra korlátozni. Vizsgáljuk meg először a hullámfelületet x₁ = 0 síkban. vagyis legyen s₁ = 0. Ezt a feltételt kihasználva a 11.64. egyenletből egyszerű számolással

(11.75)

összefüggés adódik. Ennek a két

és

(11.76)

gyöke a keresett két fázissebesség négyzete. A 11.10. ábra alapján a hullámfelület pontjaira

és

(11.77)

összefüggések teljesülnek. A 11.76. és a 11.77. egyenletekből a hullámfelületet a (x₂, x₃) síkban az

és

(11.78)

egyenletű görbék írják le. Az első egy sugarú kör, a második pedig egy negyedrendű ovális, melyet a 11.13. ábra szemléltet. A 11.74. relációk miatt az ovális teljes egészében a körön belül halad. A további két x₂ = 0 illetve az x₃ = 0 síkokra teljesen hasonlóan kapjuk a fázissebességeket. Az ezeket leíró összefüggéseket megkaphatjuk a 11.78. egyenletekből az indexek ciklikus permutációjával (azaz az indexek 1→2→3→1 irányú kölcsönös cseréjével). A hullámfelület koordinátasíkokkal való metszeteit a 11.13. ábra mutatja.

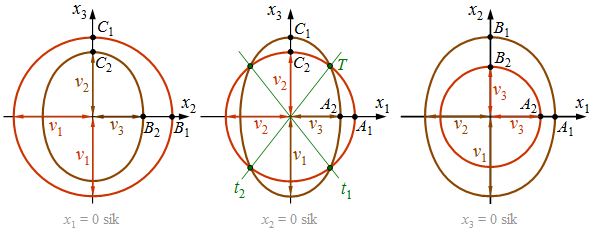11.13. ábra. Hullámfelületek metszetei a koordináta síkokkal kéttengelyű kristályban. A piros görbék körök, a barna görbék oválisok. A tengelyek hosszát nyilak jelölik. A zöld vonalak a két optikai tengelyt mutatják

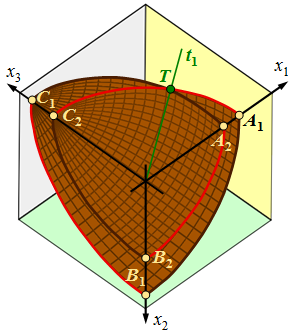
	11.14. ábra. Kéttengelyű kristályban a hullámfelület első térnyolcadba eső része hátulról szemlélve (, , ). A teljes felületet a koordináta síkokra tükrözve kapjuk meg. Az ábra jelölése megegyeznek az előző ábrán látottal.

A hullámfelület első térnyolcadba eső részét a 11.14. ábra mutatja. A koordináta síkokban lévő metszetgörbéket az előző ábrának megfelelően ábrázoltuk, és a tengelyeken lévő pontokat is feltüntettük. Általában két felület metszete egy (térbeli) görbe, azonban esetünkben a kettős héjat alkotó két felületnek mindössze 4 közös pontja van, melyek az síkban a koordináta tengelyekre szimmetrikusan, az optikai tengelyeken helyezkednek el. A 11.14. ábrán T jelöli ezek közül az egyiket.

A továbbiakban algebrai módszerrel is igazoljuk, hogy a kristályon belül csak két olyan irány van amelyre a két rezgési irányhoz tartozó két fázissebesség egyenlő, és hogy ez a két irány az síkban fekszik. Emlékeztetünk arra, hogy ez az állítás ekvivalens az index-ellipszoid szemléletes jelentésének a vizsgálatánál említett  geometriai ténnyel, hogy általában csak két olyan irány létezik, amelyre merőleges síkkal a középpontjánál elmetszve az  ellipszoidot kört kapunk, és ez a két irány a legkisebb és legnagyobb tengelyek síkjában van. Mivel a fősebességek között fennáll a 11.74. reláció, biztosan létezik olyan u > 0 és w > 0 mennyiség, melyre a

és

(11.79)

összefüggések teljesülnek. Továbbá vezessük be az v paramétert a

(11.80)

definícióval. Az v paraméter a v_p fázissebesség v₂ fősebességtől való eltérését jellemzi. Ha 0 < v, akkor v₂ < v_p, míg v < 0 esetén v_p < v₂, továbbá v = u esetén v_p = v₁, valamint v = –w teljesülésekor v_p = v₃. A fázissebességet meghatározó 11.64. egyenlet az u, w és v paraméterekkel az

(11.81)

alakba írható. Amiből a zárójelek felbontásával és a v hatványainak a kiemelésével az

(11.82)

másodfokú egyenletet kapjuk. Mivel u és w pozitívak, a 11.82. egyenlet diszkriminánsa nem negatív, azaz

.

(11.83)

Ezért az egyenletnek két valós gyöke van, melyek D = 0 esetén egyeznek meg. Jelölje a két gyököt és . Mivel a másodfokú egyenlet gyökeire fennáll a reláció, így a két gyök ellentétes előjelű vagy nulla, és az utóbbi akkor és csak akkor lehetséges, ha a két gyök egyenlő. Jelölje ′ a nem-negatív és '' a nem-pozitív gyököt, azaz

és      .

(11.84)

A 11.81. egyenlet bal oldalán álló kifejezés biztosan pozitív ha az vagy a  relációk esetén. Így az egyenlet csak akkor teljesülhet ha a gyökökre fennáll a

(11.85)

reláció. A két gyök akkor és csak akkor egyenlő, ha a 11.83. diszkrimináns zérus. Mivel a diszkrimináns két nem-negatív szám összege, az összeg zérus csak úgy lehet, ha mindkét tag külön-külön zérus. Amiből az

és

(11.86)

feltételek egyidejű fennállása következik. Az első feltétel éppen azt jelenti, hogy az azonos fázissebességekhez tartozó s irány az síkban fekszik. A második feltételt pedig az síkban csak két egyenes teljesíti. Ha β jelöli az egyenesnek a x₃ tengellyel bezárt előjeles szögét, akkor

és

(11.87)

összefüggésekkel leírt irányba lesznek a fázissebesség azonosak, azaz ezek az egyenletek szolgáltatják az optikai tengelyek irányát az síkban. A 11.87. egyenletekből és a 11.79. definíciókból következik, hogy az optikai tengelyek irányát meghatározó szögeket a

(11.88)

egyenletek adják meg.

A fázissebességeket kifejezhetjük az s hullámnormálisnak az t₁ és t₂ optikai tengelyekkel bezárt θ₁, illetve θ₂ szögével is. Az optikai tengelyek irányába mutató egységvektorokat alakba írhatjuk fel. Ha kihasználjuk, hogy mind a három szóban forgó vektor egységnyi hosszúságú, a összefüggésekhez juthatunk. A 11.86. egyenletekből következő összefüggésből egyszerűen megmutatható, hogy

     és        .

A 11.82. egyenletre felírva a másodfokú egyenlet megoldóképletét, a benne szereplő tagokat egyszerű kifejezhetjük az előző formulákat felhasználva. Ez alapján az 11.82. egyenlet megoldásai

.

A 11.79. és 11.80. összefüggéseket is figyelembe véve a fázissebességre az

(11.89)

egyenletet kapjuk. Ebből a formulából úgy tűnhet, hogy a fázissebesség nem függ a v₂ fősebességtől. Azonban az optikai tengely iránya, és ezen keresztül a θ₁ és θ₂ szögek is függnek a v₂ fősebességtől. Így nyilván a fázissebesség is függ tőle.

Az adott t egységvektorral leírt irányba a sugársebességet 11.36. egyenlet gyökei szolgáltatják. Vizsgáljuk meg a sugárfelület és a koordináta síkok metszeteit. Az x₁ = 0 síkban lévő metszetre t₁ = 0. A 11.36. egyenletből közvetlenül megkaphatjuk a metszet görbék egyenleteit. Azonban a dualitás-szabályt használva, a 11.76. egyenletből rögtön felírhatjuk a sugársebességeket. Így a

és        ,

(11.90)

a 11.76. összefüggések duális egyenletei, megadják a sugársebességek négyzeteit. A 11.10. ábra alapján a sugárfelület pontjait az (x₂, x₃) síkban

és

(11.91)

egyenletek adják meg. A 11.90. egyenleteket felhasználva a két metszetgörbét az

és

(11.92)

relációk írják le. Az első egyenlet egy v₁ sugarú kör, a másik pedig egy x₂ irányba v₃, az x₃ irányba v₂ féltengelyű ellipszis. A fősebességekre fennálló 11.74. reláció miatt az ellipszis a körön belül halad. A többi koordináta síkokra vonatkozó metszeteket a hullámfelületekhez hasonlóan az indexek ciklikus permutációjával kaphatjuk meg a 11.92. egyenletekből. A sugárfelületek metszetei hasonlítanak a hullámfelületek 11.13. ábrán látható metszeteihez, csak a negyedrendű ovális helyett egy ellipszis áll. Az (x₁, x₃) síkban a két héjnak megfelelő kör és ellipszis az optikai sugártengelyen metszi egymást. A 11.14. ábrán ábrázolt hullámfelülethez hasonlóan a sugárfelület két héjának is csak négy közös pontja van, melyek az (x₁, x₃) síkban az optikai sugártengelyeken szimmetrikusan helyezkednek el. A sugártengelyek irányát a 11.86. egyenletek duálisa, a

és

(11.93)

összefüggések határozzák meg. A második relációból a sugártengelyeknek az x₃ tengellyel bezárt γ szögére a

(11.94)

egyenlet áll fenn, ahol β a hullámnormálisokhoz tartozó optikai tengelynek x₃ tengellyel bezárt szöge.