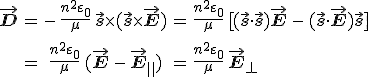Monokromatikus síkhullámok anizotróp közegben
Keressük a Maxwell-egyenleteknek az s egységvektor által megadott irányba terjedő ω körfrekvenciájú monokromatikus síkhullám megoldásait anizotróp közeget feltételezve. Ekkor komplex formalizmust használva
|
|
(11.10) |
|
|
ahol c a vákuumbeli fénysebesség, valamint c/n az s irányhoz tartozó fázissebesség, és így n a törésmutató az s irányra vonatkozólag. A 11.10. kifejezéseket az M-1 egyenletbe helyettesítve és a J = 0 feltételt kihasználva, egyszerű - az izotróp esethez hasonló számolással - a
|
|
(11.11) |
összefüggést kapjuk. Ugyanilyen módon az M-2 egyenletből és az 1.7. anyagegyenletből
|
|
(11.12) |
egyenlet adódik, amely megegyezik az izotróp esetre vonatkozó 3.5. egyenlettel, mert mágneses szempontból izotróp a közeg (csak most a vákuumbeli fénysebességet c0 helyett c jelöli). A 11.12. összefüggést a 11.11. kifejezésbe helyettesítve, és ismert vektor azonosságokat alkalmazva
|
|
(11.13) |
egyenlethez jutunk, ahol
|
|
(11.14) |
| 11.1. ábra. Az elektromágneses tér jellemzőinek (B, H, E és D) egymáshoz viszonyított iránya anizotróp közegben terjedő monokromatikus síkhullám esetén. |
az elektromos térerősség s vektorral párhuzamos illetve arra merőleges komponense, továbbá az átalakítások során kihasználtuk az ![]() relációt és s vektor egységnyi hosszát. Az elektromágneses tér jellemzőinek egymáshoz viszonyított állását a 11.1. ábra szemlélteti. Mivel a közeg mágneses szempontból izotróp B és H azonos irányú. A 11.11. egyenlet szerint D merőleges az s és a H vektorokra. A 11.12. egyenlet alapján H merőleges az s és E vektorokra. Ebből következőleg s, E és D vektorok azonos, a H vektorra merőleges síkba esnek. Az animáción az s hullámnormális sötét zöld, az elektromos térerősség világos vörös, az s irányba eső komponense világos zöld, az E és a H vektorokra merőleges Poynting-vektor irányába mutató, szintén az s , E és a D vektorok síkjában fekvő
relációt és s vektor egységnyi hosszát. Az elektromágneses tér jellemzőinek egymáshoz viszonyított állását a 11.1. ábra szemlélteti. Mivel a közeg mágneses szempontból izotróp B és H azonos irányú. A 11.11. egyenlet szerint D merőleges az s és a H vektorokra. A 11.12. egyenlet alapján H merőleges az s és E vektorokra. Ebből következőleg s, E és D vektorok azonos, a H vektorra merőleges síkba esnek. Az animáción az s hullámnormális sötét zöld, az elektromos térerősség világos vörös, az s irányba eső komponense világos zöld, az E és a H vektorokra merőleges Poynting-vektor irányába mutató, szintén az s , E és a D vektorok síkjában fekvő
|
|
(11.15) |
egységvektort sötét vörös szín jelöl. A H és a D vektorok transzverzálisak az s terjedési irányra, az E vektor viszont nem. A (D, H, s) és a (E, H, t) mindegyike jobbsodrású páronként merőleges vektorhármast alkotnak. Mivel a középső H elem közös, ezért az D és E valamint az s és t által bezárt, az ábrán kék ívvel jelölt, szögek azonosak. Továbbra is érvényes az izotróp esetben tett megállapítás, hogy az elektromos és mágneses energiasűrűség egyenlő (![]() ). Ugyanis 11.11. egyenletet és a vegyesszorzat elemeinek ciklikus permutációjára vonatkozó invarianciáját felhasználva
). Ugyanis 11.11. egyenletet és a vegyesszorzat elemeinek ciklikus permutációjára vonatkozó invarianciáját felhasználva
|
|
(11.16) |
adódik az elektromos tér energiasűrűségére, továbbá teljesen hasonló módon a 11.12. és a 1.7. egyenletek alapján
|
|
(11.17) |
a mágneses tér energiasűrűsége. Melyekből látható, hogy a két energiasűrűség valóban egyenlő, valamint a teljes energiasűrűségre
|
|
(11.18) |
a kifejezést kapjuk.
Az s és a t egységvektorok eltérő iránya miatt, anizotróp közegben az energia a hullámfelületekre merőleges s iránytól eltérő t irányba terjed. Anizotróp közegben az energiaáramlás sebessége irányban és nagyságban is különbözik a fázissebességtől. A fázissebesség c/n nagyságú és a hullámfelületre merőleges, amit vektoriálisan a
|
|
(11.19) |
formulával írhatunk le, ahol ![]() . Az energiaáramláshoz tartozó áramsűrűséget, a Poynting-vektort, az
. Az energiaáramláshoz tartozó áramsűrűséget, a Poynting-vektort, az
|
|
(11.20) |
alakba felírva bevezethetjük a
|
|
(11.21) |
ún. sugársebességet, amely az energia terjedésének az irányába mutat és ![]() nagysága megadja erre az irányra merőleges elemi felületen az energiaáramlás sebességét. A 11.18. egyenletből
nagysága megadja erre az irányra merőleges elemi felületen az energiaáramlás sebességét. A 11.18. egyenletből
|
|
(11.22) |
következik, ahol α az s és t egységvektorok által bezárt szög (és így cosα = t·s). A 11.22. formula azt mutatja, hogy a sugársebesség a hullámnormális irányba eső vetülete a fázissebességgel egyenlő. A törésmutató mintájára bevezethetjük a
|
|
(11.23) |
ún. sugárindexet (vagy energiaindexet). A ![]() és a 11.22. összefüggéseket felhasználva
és a 11.22. összefüggéseket felhasználva
| (11.24) |
egyenletet kapjuk.
Dualitás-szabály
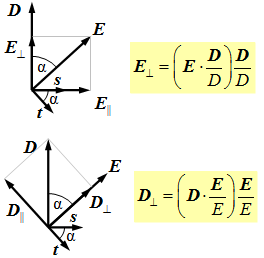 |
|
| 11.2. ábra. Az elektromos térerősség és eltolás (E és D) valamint a hullám-normális és a sugárirány (s és t) a H vektorra merőleges síkban. |
A 11.2. ábra alapján látható, hogy fennáll a
|
|
(11.25) |
reláció, amit összehasonlítva a 11.13. egyenlettel az
|
|
(11.26) |
kifejezést kapjuk. Ezt a 11.24. egyenletből adódó ![]() helyettesítve, valamint az
helyettesítve, valamint az ![]() skaláris szorzatból a cosα-t kifejezve
skaláris szorzatból a cosα-t kifejezve
| (11.27) |
formula adódik. A 11,26. és 11.27. egyenletek azt mutatják, hogy az elektromos térerősség és az eltolás együttesen már meghatározzák a törésmutatót és a sugárindexet. A törésmutatóhoz és a sugárindexhez hasonlóan az E és D vektorok az s hullámnormálist és t sugárirányt is meghatározzák. Kiindulva az
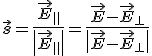 és a és a 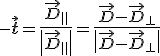 |
(11.28) |
relációkból és a merőleges komponensek 11.2. ábrán látható előállítását felhasználva egyszerű számolással az
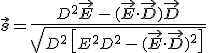 és és 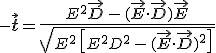 |
(11.29) |
egyenleteket kapjuk. A 11.28. és a 11.29. egyenletekből látható, hogy a két egyenlet kölcsönösen egymásba megy át, ha változókban az ![]() cserét egyidejűleg végrehajtjuk. Könnyen megmutatható, hogy a 11.25. és a 11.26. egyenletek is hasonló tulajdonsággal bírnak. A két egyenlet egymásba transzformálódik a változók
cserét egyidejűleg végrehajtjuk. Könnyen megmutatható, hogy a 11.25. és a 11.26. egyenletek is hasonló tulajdonsággal bírnak. A két egyenlet egymásba transzformálódik a változók
![]()
egyidejű cseréje során. Az egymással cserélt mennyiségeket duális változóknak nevezzük. Megmutatható, hogy a később levezett formulák is rendelkeznek a fenti tulajdonsággal. Amennyiben az 11.1. táblázat 1. sorában lévő változók között valamilyen összefüggés érvényes, akkor a változók 2. sorában az alatta található duálisával való felcserélésével továbbra is érvényes relációt kapunk. Ez az ún. dualitás-szabály.
| 11.1. táblázat. A dualitás-szabálynál említett változók és duálisaik. Az 1. sorban lévő változókat egy érvényes összefüggésben egyidejűleg a 2. sorban alattuk álló duálisaikra cseréljük, akkor továbbra is érvényes összefüggést kapunk. Az utolsó oszlopban vj a 11.33. egyenlettel definiált fősebességeket jelöli. | ||||||||||||