11. Kristályok optikája

Az eddig kifejtett izotrop közegekre vonatkozó optikai jelenségek elméleti vizsgálata kétféle egyenletrendszeren alapult: az anyagegyenleteken és a Maxwell-egyenleteken. Optikai szempontból anizotróp, azaz iránytól függő optikai tulajdonságú közegben az anyagegyenleteket kell módosítani olyan módon, hogy számot adjon az iránytól való függésről. A következőkben feltesszük, hogy a közeg az anizotróp optikai viselkedése az elektromos tértől származik, azaz mágneses szempontból a közeget izotropnak tekintjük, valamint feltételezzük, hogy a közeg átlátszó. A két utóbbi feltevés matematikai szempontból ez azt jelenti, hogy a közeg szigetelő, azaz σ = 0, valamint a mágneses térmennyiségek közötti kapcsolatot megadó 1.7. egyenletet továbbra is fennáll, ahol a μ relatív mágneses permeabilitás skalármennyiség. Az elektromos térmennyiségek közötti kapcsolatot a lehető legegyszerűbb, de az irányfüggést már magába foglaló matematikai összefüggéssel szeretnénk leírni. Az irányfüggést már leírni képes, matematikai szempontból legegyszerűbb kapcsolat, a D és az E vektorok közötti homogén és lineáris függés. A továbbiakban feltesszük, hogy az elektromos eltolás és az elektromos térerősség közötti összefüggés ilyen, azaz az fennáll közöttük az 1.3. egyenlet, ahol az ε egy másodrendű tenzor, a (relatív) dielektromos tenzor. Ismert, hogy ha vektorokat egy adott bázisban (koordináta-rendszerben) írjuk fel, akkor egy másodrendű tenzort egy 3×3-as mátrix reprezentál. Ha az x, y és z komponenseket sorrendben az 1, 2 és 3 indexekkel jelöljük, akkor koordinátákkal kiírva az 1.3. vektoregyenlet

(11.1)

összefüggésekkel fejezhető ki, ahol ε_ij a dielektromos tenzort az adott koordináta-rendszerben reprezentáló mátrix elemei és i, j = 1, 2, 3.

A továbbiakban megmutatjuk, hogy az energiamegmaradás elvéből következik, hogy a dielektromos tenzor mátrixa szimmetrikus, azaz  ε_ij = ε_ji. Csupán a Maxwell-egyenletekből, vagyis az anyagegyenletek felhasználása nélkül levezetett 1.21. egyenletből az előbb említett feltételek mellett akkor következik az energia megmaradását kifejező 1.22. kontinuitási egyenlet, ha a

(11.2)

reláció fennáll. Ezt koordinátákkal az

alakban fejezhetjük ki, ahol az idő szerinti deriválást most pont jelöli. Ebből ε₀-lal egyszerűsítve

(11.3)

egyenlet következik. A bal oldalon lévő kifejezésben először cseréljük fel a két összegző indexet, majd cseréljük fel az összegzés sorrendjét, így

.

(11.4)

A 11.3. és a 11.4. egyenletekből pedig már

(11.5)

reláció következik, amely tetszőleges E vektor esetén csak akkor teljesülhet ha

(11.6)

azaz a dielektromos tenzort reprezentáló mátrix valóban szimmetrikus.

A lineáris algebrából ismert, hogy egy szimmetrikus mátrix sajátértékei valósak. A különböző sajátértékekhez tartozó sajátvektorok merőlegesek. Mindig megadható olyan derékszögű koordináta-rendszer, amelynek bázisvektorai sajátvektorok. Ezt a koordináta-rendszert nevezzük főtengelyrendszernek. Ebben a főtengelyrendszerben a lineáris operátor mátrixa diagonális, és a főátlóban a sajátértékek vannak:

,

(11.7)

ε₁, ε₂, ε₃ sajátértékek az ún. fődielektromos állandók. Ebben a dielektromos főtengelyrendszerben a 11.1. egyenlet a

(11.8)

alakot ölti, ahol  j = 1, 2, 3. A szimmetrikus dielektromos tenzor elemeivel képzett kvadratikus alak biztosan pozitív definit, mert az elektromos tér energiasűrűsége és az egyenlőség csak a zérus vektor esetén áll fenn. Ezért a fődielektromos állandók pozitívak, továbbá a

(11.9)

egyenlettel definiált másodrendű felületet egy ellipszoid, melyet Fresnel-féle ellipszoidnak nevezünk. Az izotrop esethez hasonlóan anizotróp közegben is felléphet diszperzió. Ez nem csak a fődielektromos állandók frekvenciafüggésében mutatkozhat meg, hanem a Fresnel-ellipszoid főtengelyeinek az iránya is függhet a frekvenciától. Ez a jelenség az ú.n. főtengely-diszperzió, amely a triklin és a monoklin kristályrendszerben kristályosodó kristályoknál léphet fel, mert ezeknél a szimmetria tulajdonságok nem határozzák meg a főtengelyek irányait.
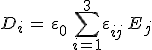
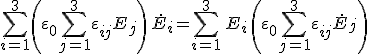
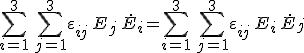
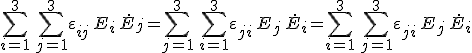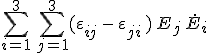
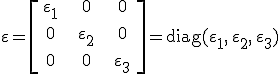