Kettős törés

	11.15. ábra. Mészpát kristályon keresztül nézve a feliratot megkettőzve látjuk. Figyeljük meg, hogy mi történik a kristály forgatása során

Ha egy papíron lévő feliratra mészpát kristályt helyezünk, és ezt a kristályon keresztül nézzük, akkor a szöveget a kettőzve látjuk. Ezt a különös, kettős törésnek nevezett jelenséget mutatja a 11.15. ábrán mészpát kristállyal végzett kísérletről készült film. A kristályt forgatása során az egyik felirat közel helyben marad, a másik felirat az előző körül körbe jár. A jelenséget az okozza, hogy - amint azt hamarosan megmutatjuk - a kristály felületét elérő fénysugár a felületen átlépve két sugárra törik meg. Mivel a kalcit kristály egytengelyű, az egyik sugár az izotróp módon terjedő, és így a Sneliius-Descartes-féle törvényt követő, ordinárius, míg a másik a Snellius-Descartes-féle törvényt nem követő extraordinárius sugár lesz. A két sugár a kristály hátulsó felületet elérve, mivel izotróp közegbe lépnek, már nem törik további két sugárra, így a kristályból két sugár lép ki. Így a kristályon keresztül nézve a tárgyakat megkettőzve látjuk.

	11.16. ábra. Kettős törés kalcit kristályon.

Azt, hogy a kristályra eső fénysugarak kettős törést szenvednek el a kristályon való áthaladás során, egy keskeny lézernyalábbal végzett, a 11.16. ábrán látható kísérlettel szemléltethetjük. Egy He-Ne lézer keskeny nyalábja a kristályon való áthaladás során két nyalábra törik. Hogy a két nyaláb elkülönülése jobban látszódjon, és a kristály hátsó felületén szóródó fény hatását csökkentsük, egy lencsével a hátsó felületet leképeztük egy ernyőre. Figyeljük meg, hogy mi történik a kristály forgatása során. A lézernyaláb hasonlóan az előző kísérletnél látott felirattal azonos módon viselkedik.

	11.17. ábra. Az "optika" szó kalcit kristályon és polarizátoron keresztül szemlélve. Figyeljük meg, hogy mi történik a polarizátor forgatása során!

Az egytengelyű kristályok  ismertetett tulajdonságai szerint mindkét hullám lineárisan poláros, és a két rezgési irány egymásra merőleges. Az extraordinárius hullámnál a rezgési irány a főmetszetben van, az ordinárius hullám esetén pedig erre merőleges. Ennek megfelelően, ha  még egy polarizátort is behelyezünk a szemünk és a kristály közé, akkor a polarizátor forgatásával a két felirat felváltva eltűnik majd ismét láthatóvá válik, ahogy az a 11.17. ábrán látható kísérlet is mutatja. A polarizációs tulajdonságokat a lencse mögé helyezett polarizátor segítségével is vizsgálhatjuk. Ezt a kísérletet mutatja a 11.18. ábrán látható három kísérletről készült film, melyek csak abban térnek el egymástól, hogy a kristály az előzőhöz helyzetéhez képest 45º-kal elforgattuk. A kísérletek során a polarizátort forgattuk. Figyeljük meg, hogy az ordinárius és extraoridinárius nyaláb milyen polarizátor állásnál tűnik el.

11.18. ábra. Polarizációs viszonyok kalcit kristályon áthaladó fénynyaláb esetén. Az egymás alatt látható három kísérletnél a kristályt a felette lévőhöz képest 45º-kal elforgattuk.

A kísérletek során látott jelenség mélyebb megértésének érdekében tekintsünk egy izotróp közegből egy optikailag anizotróp közeg sík határfelületére beeső monokromatikus síkhullámot. A továbbiakban csak a megtört hullámhoz tartozó terjedési irány meghatározását tűzzük ki célul, mivel a visszavert és a megtört hullám amplitúdóira vonatkozó reflexiós és transzmissziós tényezők (egy-egy Jones-féle mátrix elemei) a következő fejezetben ismertetett általános módszer speciális eseteként adódnak. Bizonyos speciális esetekre a Fresnel-formulákhoz hasonló kifejezések származtathatók [6]. Jelölje a beeső síkhullám terjedési irányát egységvektor, az átmenő, vagyis kristályban terjedő síkhullám terjedési irányát egységvektor. Vegyük fel a vonatkoztatási rendszert a már megvizsgált izotróp esettel azonos módon, azaz legyen a határfelület a z = 0 sík, továbbá legyen az izotróp közeg a z < 0, az anizotróp közeg pedig a z > 0 tartományban. A határfelületen előírt feltételek - az izotróp esetben fennálló 5.1. egyenlethez hasonlóan - csak akkor teljesülnek, ha a határfelület minden r = (x, y, 0) pontjában minden t időpontban fennáll a

(11.95)

egyenlet, ahol és a beeső illetve az átmenő hullám fázisebességeit jelölik. Ebből pedig következik, hogy az

(11.96)

összefüggés áll fenn. Ami azt mutatja, hogy

,

(11.97)

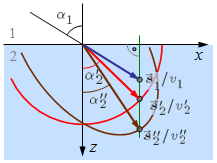
	11.19. ábra. A kettős törés értelmezése. A kristályban terjedő síkhullám normálisainak irányát a piros és a barna vektorok adják meg.

vagyis az  különbségvektor merőleges a határfelületre. Ha határfelületen lévő origóból felmérjük a kristályon belül minden irányba az adott irányhoz tartozó fázissebesség reciprok értékével egyenlő, azaz hosszúságú szakaszt, akkor egy kéthéjú felületet kapunk, mert bármely irányba két,  és  fázissebesség megengedett. Ez a kettős héjú felület az ún. inverz-hullámfelület, a konstrukció alapján nyilván a sugárfelület duális felülete, és ennek megfelelően negyedrendű felület. Az inverz-hullámfelület segítségével könnyen meghatározhatjuk a kristályon belül terjedő két síkhullám és hullámnormálisának irányát. A 11.97. összefüggésből következik, hogy a beeső síkhullám terjedési irányába mutató vektor végpontjából a határfelületre merőleges egyenesnek a kéthéjú inverz-hullámfelületen lévő két metszéspontja éppen a keresett  és vektorok végpontjai. Így a keresett hullámnormálisok irányát ezek a metszéspontok adják meg. A 11.19. ábra azt az esetet szemlélteti mikor a két optikai tengely a beesési síkban van. Egyszerűen megmutatható, hogy a dielektromos főtengely-rendszerben az inverz-hullámfelület x₂ = 0 síkkal vett metszetei az

és

(11.98)

egyenletű görbék, azaz egy sugarú kör, valamint egy és féltengely hosszúságú ellipszis. A két görbe a fősebességek közötti viszony miatt metszi egymást, és metszéspontok az optikai tengelyen vannak. A 11.98. egyenletű kört illetve ellipszist piros illetve barna színnel jelöltük a  11.19. ábrán. A másik két koordináta síkbeli metszetgörbék egyenleteit megkaphatjuk a 11.98. egyenletekből az indexek ciklikus permutációjával.

A 11.96. egyenletet koordinátákkal kiírva az

(11.99)

összefüggést kapjuk, ahol az x és y indexek a hullámnormálisok koordinátáira utalnak. Az egyszerűség kedvéért a jobb oldalon a két esetre utaló ' és '' jelöléseket elhagytuk, mert a 11.99. egyenlet minkét hullámnormálisra teljesül a neki megfelelő fázissebességgel. A továbbiakban hasonlóan járunk el a többi összefüggésnél is, azaz a megkülönböztető vesszős jelzést elhagyjuk, ha az egyenlet a mindkét hullámra érvényes. A 11.98. egyenlet tetszőleges (x, y) értékekre teljesülnek, így az 5.3. egyenletekhez hasonlóan ezekből a

és

(11.100)

kifejezések következnek. Mivel a koordináta-rendszer speciális választása miatt , így , ami azt jelenti, hogy mindkét hullámnormális a beesési síkban van. A 11.100. első egyenletét a 11.19. ábrán látható beesési és törési szögekkel formálisan az Snellius-Descartes-féle törvényre emlékeztető

(11.101)

alakra hozhatjuk. Azonban érdemes megjegyezni, hogy az izotróp esettől eltérően, most a jobb oldalon álló kifejezés függ az α₁ beesési szögtől!