Interferencia amplitúdóosztással

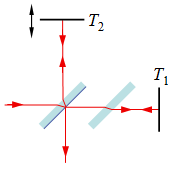
	9.8. ábra. A Michelson- interferométer vázlata.

A Michelson-féle interferométer vázlatát a 9.8. ábra szemlélteti. A beeső fénynyalábot egy vékony üveglemez hátsó felületére felvitt vékony ezüst film két nyalábra osztja. A fény egy része visszaverődik az ezüst filmről, a másik része pedig áthalad rajta. Az interferométer két karjában haladó nyalábokat a T₁ és a T₂ síktükörrel visszafordítjuk. Ezeket a visszavert nyalábokat a nyalábosztó lemez ismét egyesíti, így az interferométer kimenetén a két kar optikai úthossz különbségének megfelelően interferencia lép fel. A nyalábosztón keresztül haladó nyaláb karjában célszerű a nyalábosztó lemezzel azonos kompenzátor lemezt elhelyezni, hogy kompenzálja a másik karban az üveglemezen kétszer áthaladó  nyalábnál fellépő fázistolást. Tegyük fel, hogy a nyalábosztó 50-50%-ban osztja szét a nyalábokat. Ekkor a kimeneten a

(9.34)

időbeli késéstől eltekintve, két azonos nyaláb jelenik meg, ahol Δ₁ és Δ₂ a két karban való terjedéshez tartozó optikai úthosszak és c a vákuumbeli fénysebesség. Így a kimenet egy adott helyen a

(9.35)

formula adja meg a térerősséget, ahol a E₁ az T₁ tükörről visszavert nyaláb térerőssége. Ezért az interferenciát jellemző 9.21. kölcsönös koherencia függvény esetünkben a

(9.36)

autokorrelációs függvény. Az intenzitásra a 9.22. és 9.23. összefüggéseket felhasználva

(9.37)

egyenlet adódik, ahol I₁ az 1. karból kilépő nyaláb intenzitása. Könnyen ellenőrizhető, hogy az monokromatikus esetre

(9.38)

kifejezés adja meg az autokorrelációs függvényt, amiből a 9.34. egyenletet figyelembe véve

(9.39)

formula írja le a komplex koherenciafokot, ahol

(9.40)

a két találkozó hullám fáziskülönbsége, ahol λ a vákuumbeli hullámhossz. A 9.39. és a 9.40. egyenleteket a 9.37. kifejezésbe helyettesítve, egyszerű trigonometrikus átalakítással az

(9.41)

egyenletet kapjuk az intenzitásra. Ez formailag megegyezik a Young-féle kettős résnél levezetett 9.31. összefüggéssel. Így az intenzitás is ugyanúgy függ a T₂ tükör mozgatásakor a tükör helyzetétől. Ha x jelöli a tükör helyzetét leíró koordinátát, és az x = 0 tartozik az azonos karhosszúsághoz , akkor az intenzitás a 9.3. ábrán látható módon függ a T₂ tükör helyzetétől, ha az x koordinátát a λ/(2n) egységekben mérjük, ahol n az interferométert kitöltő közeg törésmutatója. Nem teljesen koherens esetre is, az ennek megfelelő, piros görbe írja le az intenzitás függését a tükör helyzetének a függvényében a 9.32. komplex koherenciafokot feltételezve.

Ha az interferométert síkhullámmal (kollimált nyalábbal) világítjuk meg, és valamelyik tükröt a 9.8. ábra síkjára merőleges tengely körül kissé elforgatjuk, akkor a kimeneten a terjedési irányra merőleges síkban a forgástengellyel párhuzamos interferenciacsíkok mutatkoznak, melyek intenzitását a csíkokra merőleges irányban a 9.41. egyenlet ír le. A megfigyelési síkban az fogástengellyel párhuzamos egyenesen az útkülönbség állandó így ezekhez azonos fényintenzitás tartozik. A forgástengelyre merőleges egyenesen mentén pedig a forgatás szögével arányosan változik az útkülönbség. Ha az interferométert divergens nyalábbal világítjuk ki és a tükrök merőlegesen állnak a karok irányára, akkor koncentrikus interferencia gyűrűk jelennek meg, melyek az azonos szögben beeső sugarak hoznak létre.

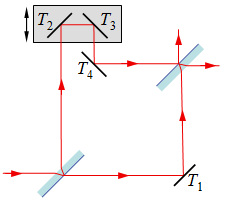
	9.9. ábra. A Mach-Zehnder-féle interferométer vázlata.

A Michelson-interferométeren kívül még egy, az alkalmazásoknál gyakran használt interferométert, a 9.9. ábrán vázolt Mach-Zehnder-interferométert vizsgálunk meg. A beeső nyalábot egy nyalábosztó amplitúdó osztással két nyalábra bontja, melyeket az interferométer két karjában terjednek, irányukat síktükrökkel állíthatjuk. A T₂ és T₃ tükrök együttes, a nyíllal jelölt irányban, való mozgatásával az egyik kar hossza változtatható. A két karban terjedő nyalábokat a nyalábosztóval azonos lemez ismét egyesíti. A kimeneten a két kar közötti optikai úthosszkülönbségnek megfelelő interferenciát észlelhetünk. A Michelson-interferométerre vonatkozó formulák most is érvényesek. Így az intenzitást a 9.3. ábrán látható grafikonok írják le, ha x jelöli a T₂ és T₃ tükrök helyzetét megadó koordinátát és a λ/(2n) egységeket használunk a vízszintes tengelyen. Az x = 0 eset itt is az egyenlő karhosszhoz tartozik. Ahogy az 9.9. ábrán is látható, az interferométernek két kimenete van, amely néhány esetben előnyös lehet.

	9.10. ábra. Vízfelszínén lévő vékony olajfilmen látható színes interferencia mintázatok. Az olaj esős időben parkoló autóból fojt a vizes burkolatra. Az autó kereke jobbra látható.

Fehér fénnyel megvilágított szappanhártyára bizonyos irányból ránézve színes mintázatokat láthatunk. Hasonlóan elszíneződéseket láthatunk vízfelületen úszó vékony olajfilmre ránézve. A 9.10. ábrán esős időben parkoló autó mellett az útburkolatról készült fénykép látható. Az autóból olaj szivárgott nedves útburkolatra, amelyen szétterülve egy vékony olajfilm alakult ki. Látni fogjuk, hogy a film alsó illetve felső felületéről visszaverődő hullámok közötti interferencia következtében bizonyos irányból beeső hullámok a hullámhosszuktól függően erősíthetik vagy gyengíthetik egymást. Ennek megfelelően a beeső fehér fényt eredményező spektrális súlyok a hullámhossztól függően megváltoznak, amely fényérzetünkben elszíneződésként mutatkoznak meg. Az ilyen sík-párhuzamos rétegeken kialakuló interferencia sok optikai eszköz működésének megértése szempontjából fontos. Az egyszerűbb esetek, néhány rétegből álló rendszer az egyes határrétegekre alkalmazva a Fresnel-féle formulákat, még szemléletesen tárgyalhatók. Az összetettebb rétegrendszerek a 6. fejezetben ismertetett karakterisztikus mátrixon alapuló eljárással könnyen leírhatók. Ez az eljárás magába foglalja az interferencia hatását. Például láttuk, hogy egy lemez reflexiós tényezője a lemezvastagságával periodikusan változik. Ezt a tulajdonságot is a lemez alsó és felső felületéről visszaverődő hullámok interferenciájával magyarázhatjuk személetesen. Hasonlóan, gyengítő interferenciával értelmezhetjük a reflexiómentesítő réteg működését is.

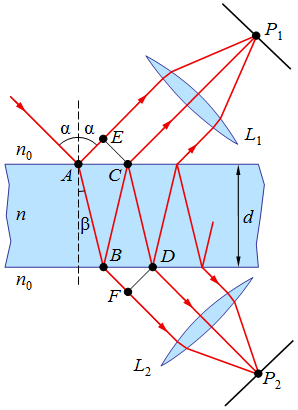
	9.11. ábra. Sík-párhuzamos lemezre α szögben beeső hullámból a két határfelületen való visszaverődések és törések miatt, amplitúdó osztással több hullám alakul ki, melyeket egy gyűjtő lencsével a fókuszsík egy pontjába összegyűjthetünk.

Sík-párhuzamos lemezen kialakuló interferencia jelenségek vizsgálata céljából tekintsük a 9.11. ábrán látható elrendezést. Essen egy n₀ törésmutatójú közegben lévő n törésmutatójú, d vastagságú sík-párhuzamos lemezre α szögben egy monokromatikus fénynyaláb.  A lemez felső felületén a fény egy része visszaverődik, másik része tovább halad. Ezt a tovaterjedő nyalábot az alsó felület szintén egy visszavert és egy átmenő nyalábra bontja. Az alul visszavert nyaláb a felső felületen megint két nyalábra osztódik. Így a leírt módon a két határfelületen a visszaverődések és törések következtében, amplitúdó osztással, mind az átmenő mind a visszavert fény esetén azonos irányban terjedő hullámok jönnek létre. Ezeket egy lencse segítségével a fókuszsík egy pontjába gyűjthetjük össze. A kialakuló interferencia jellegét a hullámok közötti optikai úthosszkülönbség határozza meg. Két szomszédos sugárral reprezentált hullám intenzitásainak arányát a Fresnel-formulák segítségével számolhatjuk ki. Ha törésmutatók különbsége nem túl nagy, és a beesési szög is kicsi, akkor a reflexiós tényező is kicsi. Ilyen esetben gyakorlatilag elegendő, mind a visszavert, mind az átmenő fény esetén az első két sugarat figyelembe venni. Ekkor gyakorlatilag az interferencia kétsugarasnak tekinthető. Ha a felületek reflexiós együtthatója nagy, akkor az interferencia már többsugarasnak tekintendő. A reflexiós tényezőt a beesési szög növelésével, vagy a törésmutatók különbségének növelésével, illetve a felületeknek vékony tükröző fém- vagy dielektrikum réteggel való bevonásával emelhetjük meg.

Számoljuk ki először két szomszédos sugárral reprezentált hullámok közötti fáziskülönbséget. A lencse képalkotási tulajdonságai miatt az EP₁ és CP₁ utakra az optikai úthosszak azonosak, így az optikai úthosszkülönbség visszavert fényben az első második sugár között

.

(9.42)

A 9.11. ábráról látható, hogy a harmadik és a második, és a további belső reflexiók következtében létre jött szomszédos sugarakkal reprezentált hullámok között szintén 9.42. egyenletnek megfelelő optikai úthosszkülönbség áll fenn. Hasonlóan könnyen látható, hogy átmenő fényben két szomszédos sugárra is ugyanez az optikai úthosszkülönbség. Geometriai megfontolásokat és a Snellius-Descartes-törvényt felhasználva egyszerűen megmutatható, hogy

.

(9.43)

Az második alakból jól látható, hogy az optikai úthosszkülönbség adott törésmutatók és lemezvastagság esetén a beesési szögtől függ. Azonos beesési szögű nyalábokhoz azonos optikai úthosszkülönbség tartozik, így ezek ugyanolyan fényhatást hoznak létre az interferencia során. Ezért a lencse fókuszsíkjában kialakuló görbéket az azonos beesés görbéinek hívjuk.

A beeső hullámot felbonthatjuk egy s- és p-polarizált hullám összegére. Már láttuk, hogy a két komponens egymást nem befolyásolva terjed. A határfelületek amplitúdókra vonatkozó reflexiós és transzmissziós tényezőit a Fresnel-fomulákból számolhatjuk ki. A jelölés egyszerűsítése végett a polarizációra utaló s illetve a p indexeket elhagyjuk. Jelölje a beeső hullám elektromos térerősségének komplex amplitúdóját E₀, az (n₀, n) határfelületnek amplitúdókra vonatkozó reflexiós és transzmissziós tényezőit r és t, az (n, n₀) határfelületét pedig r' és t'. A reflexiós tényezőkre vonatkozó Fresnel-fomulákból következik, hogy

.

(9.44)

A felső felületről visszavert hullám, valamint az átlépő hullám lemezen belüli visszaverődései és kilépései következtében, visszavert fényben az

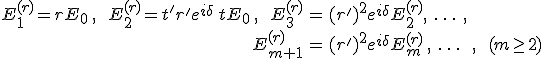(9.45)

komplex amplitúdójú hullámok, átmenő fényben pedig az

(9.46)

komplex amplitúdójú hullámok jönnek létre, ahol φ az AB szakaszon a lemezbeli tejedést leíró fázistolás, és

(9.47)

a szomszédos sugarakkal reprezentált hullámok közötti fáziskülönbség. A 9.44. és 9.45. egyenleteket felhasználva visszavert fényre az

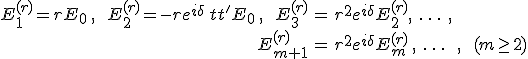(9.48)

komplex amplitúdójú hullámok lépnek fel. Amiből látható, hogy az 1. hullám a többitől előjelben különbözik, amely π fáziskülönbséget jelent. Ez a fáziskülönbség az optikailag sűrűbb közeg határán fellépő - a Fresnel-fomulákból következő - π fázisugrás következtében jön létre. A 9.46. és 9.48. egyenletek kvantitatív módon mutatja a már említett tényt, hogy kis reflexiós tényező esetén elegendő gyakorlatilag két sugár figyelembe vétele, mert az egymást követő tagok térerőssége -tel arányosan, mértani sor szerint csökken. Továbbá kicsi r esetén t·t' egyhez közeli érték. Így az első két visszavert hullám amplitúdója gyakorlatilag megegyezik, aminek következtében az interferencia minimuma gyakorlatilag zérus lesz. Így reflektált fényben, bár kicsi az interferencia jelenség maximális intenzitása, mégis a közel zérus minimum miatt közel egységnyi a láthatóság. Vagyis visszavert fényben bár fényszegény, de kontrasztos az interferencia. A 9.46. egyenletek szerint átmenő fényben az 1. és 2. hullám amplitúdója nem közel azonos, hanem arányú. Így intenzitás a minimuma közel lesz a maximhoz, amely az interferencia láthatóságát csökkenti. Így átmenő fényben a jelenség fényerős, de a kontrasztja rossz. A visszavert fényben az egyik hullámnál fellépő π fázisugrás miatt a visszavert és az átmenő fényben kialakuló interferencia egymás komplementere lesz. Ez azt jelenti, hogy ha visszavert fényben a maximális erősítést figyelhetünk meg, akkor ármenő fényben pedig maximális gyengítést tapasztalunk, és megfordítva.

A 9.46. és 9.48. egyenletekből már kiszámolhatjuk a koherens hullámok interferenciája útján kialakuló visszavert illetve átengedett hullámok komplex amplitúdóit. Koherens esetben a térerősség összegződnek, így az átmenő hullám komplex amplitúdóját az

(9.49)

formula adja meg, míg a visszavert hullám amplitúdója az

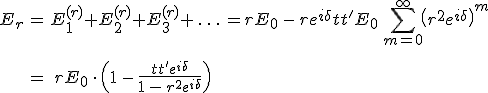(9.50)

egyenletből számítható ki, ahol a 9.49. egyenletnél kihasználtuk a 9.44. összefüggést, valamint az utolsó átalakításoknál a mértani sor összegképletét alkalmaztuk. Elnyelés hiányában fennáll az energia megmaradását kifejező

(9.51)

összefüggés, ahol és a fényenergiákra vonatkozó reflexiós illetve transzmissziós tényezők. A 9.51. egyenletet felhasználva az átmenő és a visszavert hullámok komplex amplitúdóit (a 9.49. és 9.50. egyenleteket) az

és

(9.52)

alakban írhatjuk át. A 9.52. egyenletekből már kiszámolhatjuk - az összefüggést felhasználva - az átmenő, illetve a visszavert fény intenzitását. A trigonometrikus azonosságot alkalmazva az

és

(9.53)

összefüggéseket nyerjük az átengedett, illetve a visszavert fény intenzitására, ahol az

(9.54)

paraméter határozza meg a grafikonok jellegét. Az átengedett és a visszavert fény intenzitását a 9.12. ábrán látható grafikonok szemléltetik a fáziskülönbség függvényében. Az animáció során az  reflexiós együttható (és vele együtt az F paraméter értéke is) változik. Az átengedett fény intenzitását a piros (felül), a visszavert fény intenzitását a kék görbe (alul) szemlélteti. Az grafikonon jól látható a két görbe, és velük együtt a hozzájuk tartozó interferenciák komplementer jellege.

9.12. ábra. Interferencia sík-párhuzamos lemezen. Az átengedett és a visszavert fény intenzitása a felületek R reflexiós tényezőjének különböző értékeire.

Ha az reflexiós tényező kicsi, akkor az F paraméter is kicsi, így a 9.53. kifejezésekben a törteket hatványsorba fejtve, és a lineáris tagot megtartva, az

és

(9.55)

összefüggéseket kaphatjuk az átengedett és a visszavert fény intenzitására. Ezekben a δ fáziskülönbségtől való függést a 9.10. egyenlethez hasonlóan a cosδ tényező írja le, amely azt mutatja, hogy - összhangban a már említett ténnyel - ekkor az interferencia lényegében kétsugarasnak tekinthető. A reflexiós tényező növekedésével a soksugaras interferenciának köszönhetően az átengedett fény maximumaihoz tartozó csúcsok egyre keskenyebbek lesznek. Ezért a soksugaras interferencia különösen fontos jelentőséggel bír. A soksugaras interferencián alapuló eszközök, például a Fabry-Perot-interferométer vagy a Lummer-Gehrcke-lemez spektroszkópiai alkalmazásai nagyon fontosak [1]. Divergens fényt használva a 9.12. ábrán látható csúcsok a leképező lencse fókuszsíkjában gyűrűknek felelnek meg. Ha a reflexiós tényező egyhez közeli, akkor ezek a gyűrűk nagyon keskenyek. Így nem-monokromatikus fényt alkalmazva a különböző hullámhosszakhoz tartozó gyűrűrendszerek jól megkülönböztethetők. Ennek következtében az eszköz spektrális felbontóképessége nagy lesz [1].

	9.13. ábra. Színes interferencia csíkok ék alakú folyadék hártyán.

Ék alakú lemezre eső hullám a felső felületen amplitúdó osztással két hullámra osztódik. A tovább haladó hullám egy része az alsó felületen visszaverődik, majd az éken ismét keresztül haladva, egy része kilép a felső felületen a lemezből. Ha a reflexiós tényező kicsi, akkor további belső amplitúdó osztással létrejövő reflektált hullámok hatása elhanyagolható. Így az ékről visszavert fényhullám két hullám szuperpozíciója, de mivel a lemez ék alakú, a két hullám egymással szöget bezárva terjed. Az ék alakú lemezre ránézve, a megfigyelési iránytól függően, a lemez alatt vagy felett - az ék élével párhuzamos - interferencia csíkokat láthatunk. Ilyen interferencia csíkokat szemléltet a 9.13. ábra, ahol a nehézségi erő miatt lefele növekedő vastagságú szappanhártya látható két fapálcika és a fonaldarabok által alkotott keretben. Mivel a megvilágító fény fehér, az interferencia csíkok, a színkeverés következtében színesek lesznek. Ilyen ék alakú lemezen történő interferencia jelenség megfigyeléséhez érdemes kis apertúrájú lencsét használni (erre a célra a szemünk teljesen megfelelő), mert ekkor a lemezfelületének egy adott részéről lényegében azonos szög alatt beeső sugarak érkeznek a lencsére, így az interferáló hullámok fáziskülönbségét lényegében a lemez vastagsága határozza meg. Az azonos vastagságú helyek azonos fényhatást keltenek, ezért a megfigyelhető interferencia csíkokat az azonos vastagság görbéinek nevezzük.

Az interferencia mintázat lokalizációját a 9.14. ábra szemlélteti. Ha az interferencia létrehozásában az a₁ és b₁ sugarakkal reprezentált hullámok vesznek részt, akkor az a₁ sugárral reprezentált hullámból amplitúdó osztással keletkezett hullámok az L₁ lencse képsíkjának C₁ pontjában, a b₁ sugárral reprezentált hullámból létrejövő hullámok pedig a D₁ pontban találkoznak. Ha az L₁ lencse a szemlencséket szimbolizálja, akkor az adott helyről a lemezre tekintve, a lemez alatt látjuk lebegni az interferencia csíkokat. Ha az interferencia létrehozásában az a₂ és b₂ sugarak vesznek részt, akkor a megfelelő irányból a lemezre tekintve, a lemez felett - az A₂ és B₂ pontokkal meghatározott helyeken - látjuk a csíkokat.

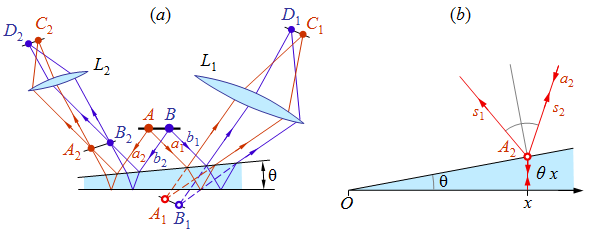9.14. ábra. Interferencia ék alakú lemezen lemezen. Az interferencia mintázat lokalizációjának szemléltetése.

A csíkok távolságát arra a legegyszerűbb esetre számoljuk ki, mikor úgy tekintünk a lemezre, hogy az alsó felületre merőlegesen esik a hullám. Ekkor a csíkokat éppen - a 9.14. ábra (b) része alapján - a lemez felületén látjuk, mert az A₂ metszéspont éppen a lemez felületére esik. Az s₁ és az s₂ sugarakra a képpontig azonos az optikai úthossz, ezért a két sugárral reprezentált hullám között a optikai útkülönbség

,

(9.56)

ahol d a lemez vastagsága az x helyen, amit θx kifejezéssel közelítünk, mert általában ék θ szöge kicsi. A maximális erősítés feltétele , a maximális gyengítés feltétele pedig , ahol m pozitív egész és λ a vákuumbeli hullámhossz. Visszavert fényben azonban még figyelembe kell vennünk az optikailag sűrűbb közeg határán fellépő π fázisugrást, amely ±λ/2 útkülönbségnek felel meg. Így visszavert fényre az erősítés és a gyengítés feltétele felcserélődik. A fázisugrás következtében a visszavert és az átmenő fényben megfigyelhető interferencia jelenségek egymás komplementerei lesznek. Így visszavert fényre, a fázisugrást is figyelembe véve, a 9.56. egyenlet alapján a sötét (s), valamint a világos (v) csíkok helyét

és

(9.57)

az  összefüggések szolgáltatják, amiből a csíkok távolsága .

Ha egy sík üveglapra egy sík-domború lencsét helyezünk, és fehér fénnyel felülről megvilágítjuk, akkor az két felület érintkezési pontja körül színes, nem egyenközű gyűrűket, a Newton által is megfigyelt Newton-gyűrűket láthatjuk. A jelenséget a 9.15. ábrán láthatjuk. Visszavert fényben középen sötét folt van az optikailag sűrűbb közeg határfelületéről visszaverődő hullámnál megjelenő fázisugrás miatt. Ezek a gyűrűk a lencse és a üveglemez közötti változó hajlásszögű levegő éken létrejövő azonos vastagság körbéi. A gyűrűk nem egyenközű volta a változó hajlásszögnek a következménye.

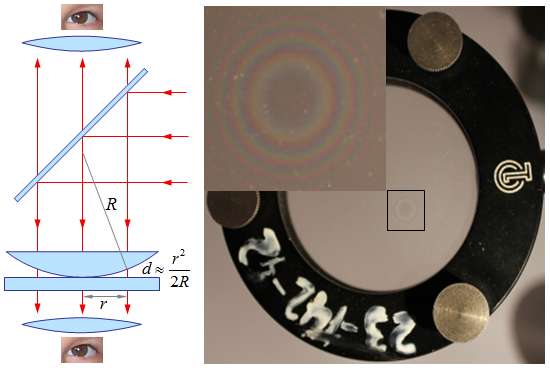9.15. ábra. Sík üveglap és a reá helyezett sík-domború lencse között kialakuló változó hajlásszögű levegő éken az azonos vastagság görbéit láthatjuk. Ezek az ún. Newton-féle gyűrűk (jobbra). A kísérletről készült kép bal felső sarkában a bekeretezett tartományt nagyítottuk ki.

A levegő ék vastagsága a középpontól r távolságra a formulával közelíthető. Így visszavert fényben, az üveglapról visszavert hullámnál fellépő fázisugrást is figyelembe véve, a gyengítés, illetve az erősítés feltételei sorrendben és , ahol és n_l a levegő törésmutatója. Amiből a visszavert fényben a sötét illetve világos gyűrűk sugarát a

és

(9.58)

kifejezések adják meg, ahol n_l helyére gyakorlatban sokszor 1 helyettesíthető. Átmenő fényben a jelenség komplementerét figyelhetjük meg. Ekkor a gyűrűk láthatósága rosszabb, mert a sík-párhuzamos lemezhez hasonlóan az interferáló hullámok amplitúdója jelentősen különbözik egymástól. Így a gyűrűrendszer egy világos homogén foltra rakódik rá, amely rontja a kontrasztot. A 9.58. egyenletek szerint a gyűrűk valóban nem egyenközűek. A kísérletből is látható, hogy növekvő m rendszámmal a gyűrűk sűrűbben helyezkednek el. Fehér fénnyel interferenciát csak közvetlenül a középpont körül láthatunk, mert belülről kifele haladva az útkülönbség négyzetesen növekszik, így viszonylag hamar meghaladja a néhány mikron koherenciahosszat.