Hullám- és sugárfelület

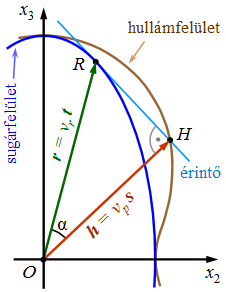
	11.10. ábra. A sugár- és a hullám-felület síkmetszete a dielektromos főtengelyek (x2, x3) síkjában.

Ha a kristály egy rögzített O pontjából minden irányba felmérjük a két rezgési iránynak megfelelő  fázissebesség vektorokat (11.19. egyenlet), akkor egy kéthéjú felületet kapunk. Ezt a felületet hullámnormális-felületnek, vagy egyszerűn csak hullámfelületnek nevezzük. Az eljárást a 11.21. egyenlettel adott  sugársebességekkel megismételve az ugyancsak kéthéjú sugárfelülethez jutunk. A sugár- illetve hullámfelület egy-egy héjának síkmetszetét a 10.10. ábra szemlélteti. Általában a sugárfelület negyed-, míg a hullámfelület hatodrendű felület. A két felület rendje azért sem azonos, mert ezek nem egymás duálisai. A 10.1. táblázat alapján a sebességek reciproka a duális változó, így a duális felület esetén a másik sebesség reciprok értéknek megfelelő szakaszt kellene felmérni az adott irányban.

A sugár- és hullámfelületek között nagyon érdekes geometriai kapcsolat áll fenn. Ennek feltárásának érdekében induljunk ki az

(11.58)

összefüggésből, amely a 11.13. egyenlet duálisa. Ezt ha megszorozzuk -tel és kihasználjuk, hogy és , akkor az

(11.59)

relációhoz jutunk. A sugárfelület pontjait éppen azok az r vektorok jelölik ki, melyek ennek az egyenletnek tesznek eleget, hiszen a sugársebességet meghatározó 11.36. sugáregyenlet is ennek a következménye. Ha sugárfelületen kicsit elmozdulunk az R pontból, akkor az E térerősség, a D eltolás és az r vektor egy kicsit megváltozik. Legyenek ezen mennyiségek megváltozásai sorrendben dE, dD és dr. Mivel a felületen mozdulunk el, és az elmozdulás infinitezimálisan kicsiny, a dr vektor az sugárfelület R pontjának érintősíkjában van. Mivel a felület pontjaira fennáll a 11.59. egyenlet, a kicsiny változások közötti kapcsolatot ennek differenciálja adja meg. Az összegre és a szorzatra vonatkozó differenciálási szabály alapján

(11.60)

az összefüggés áll fenn.  Ezt D-vel skalárisan szorozva és rendezve a

(11.61)

relációt kapjuk. Az első szögletes zárójelben lévő tag éppen a 11.59. összefüggés jobboldalával azonos, továbbá a 11.61. kifejezés bal oldalán álló tagot főtengely-rendszerben átalakíthatjuk a

módon. Így a 11.61. összefüggés az

formába alakítható át. Ebből pedig már látható, hogy a jobboldali második skaláris szorzat zérus. A szögletes zárójelben lévő vektort a vektoriális szorzatra vonatkozó azonossággal átalakítva az

(11.62)

egyenletet kapjuk. A 11.1. és a 11.2. ábrák alapján egyszerűen látható, hogy a  vektor az vektorral párhuzamos, így 11.62. szerint

(11.63)

összefüggés áll fenn, ami pontosan azt jelenti, hogy a hullámnormális merőleges a sugárfelület R pontbeli érintő síkjára. Az 11.22. egyenlet alapján , így az síkban fekvő ORH derékszögű háromszögre (lásd a 11.10. ábrát) teljesül . Ami azt jelenti, hogy a fázissebesség vektor H végpontja az érintősíkban van.

Azaz eredményünket tömören összefoglalva: megmutattuk. hogy a sugárfelületet egy adott t sugárirányban lévő R pontbeli érintősíkjára a (t-hez tartozó) s hullámnormális merőleges és vektor H végpontja az érintősíkban van. Az ilyen geometriai viszony teljesülése estén azt mondjuk, hogy a hullámfelület a sugárfelület talppontfelülete. A 11.10. ábra a felületeknek egy síkmetszete, így a hullámfelületet reprezentáló görbe a sugárfelületnek megfelelő görbének a talppontgörbéje. Az alábbi animáció a két görbe kapcsolatát szemlélteti. Később látni fogjuk, hogy a sugárfelület metszete az (x₂, x₃) síkban egy ellipszis, melynek az x₂ és x₃ irányú féltengelyeinek hossza (sorrendben) a v₃ és v₂ fősebességek (v₃ < v₂). Az animáción a tengelyek hosszát a kék színű végpontjaik mozgatásával változtathatjuk. Az animálás jelölő négyzetbe kattintva az R pont végig fut a görbén és a program kirajzolja a hozzátartozó H talppontot. Az ábrát a ctrl-F billentyű paranccsal törölhetjük.

Egy adott irányhoz tartozó terjedési sebességeket a Fresnel-féle sebességi egyenletek gyökei szolgáltatják. A fázissebesség vizsgálatának érdekében szorozzuk meg a 11.34. egyenletet a három nevező szorzatával. Így a 

(11.64)

kifejezést kapjuk. Először a matematikai szempontból egyszerűbb esetet, az egytengelyű kristályokat fogjuk vizsgálni.