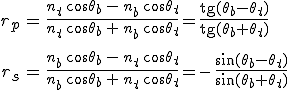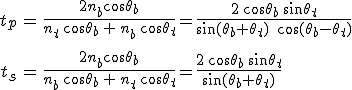Reflexiós és transzmissziós tényezők
Az amplitúdókra vonakozó együtthatók
A p és az s komponensekre vonatkozólag visszavert és a beeső hullámok amplitúdóinak az
| (5.15a-b) |
hányadosát a felület amplitúdókra vonatkozó reflexiós (vagy visszaverő) tényezőjének nevezzük. Hasonlóan az átengedett és a beeső hullám amplitúdóinak a
| (5.16a-b) |
hányadosát a felület amplitúdókra vonatkozó transzmissziós (vagy áteresztő) tényezőjének hívjuk. Ezeket a Fresnel-formulákból könnyen kiszámíthatjuk.
Az Snellius-Descartes-féle törvényt és a
![]()
trigonometrikus azonosságokat felhasználva, egyszerű számolással a Fresnel-formulákat átírhatjuk olyan alakban, melyekben csak a szögek szerepelnek. Ezeket végig számolva az amplitúdókra vonatkozó reflexiós és az transzmissziós együtthatókat
|
|
(5.17a-d) |
formulák adják meg.
Az 5.17. formulákból számolt reflexiós tényezőket ![]() relatív törésmutatót feltételezve az 5.3. ábra szemlélteti. Az ábra bal oldalán az amplitúdóra, míg a jobb oldalán a fényteljesítményre vonatkozó reflexiós és transzmissziós együtthatók láthatók. Az átmenő fény esetén a teljesítményre vonatkozó együtthatók kiszámolásánál figyelembe kell venni, hogy törés miatt a beeső nyaláb qb, és az átmenő nyaláb qt keresztmetszete között a
relatív törésmutatót feltételezve az 5.3. ábra szemlélteti. Az ábra bal oldalán az amplitúdóra, míg a jobb oldalán a fényteljesítményre vonatkozó reflexiós és transzmissziós együtthatók láthatók. Az átmenő fény esetén a teljesítményre vonatkozó együtthatók kiszámolásánál figyelembe kell venni, hogy törés miatt a beeső nyaláb qb, és az átmenő nyaláb qt keresztmetszete között a ![]() összefüggés áll fenn, továbbá a felület két oldalán a hullámellenállások eltérnek, amit a keresztmetszeten átáramló energia kiszámításánál is figyelembe kell venni (lásd a 3.13a egyenletet). Egyszerűen megmutatható, hogy a fényteljesítményekre vonatkozó
összefüggés áll fenn, továbbá a felület két oldalán a hullámellenállások eltérnek, amit a keresztmetszeten átáramló energia kiszámításánál is figyelembe kell venni (lásd a 3.13a egyenletet). Egyszerűen megmutatható, hogy a fényteljesítményekre vonatkozó ![]() reflexiós és
reflexiós és ![]() transzmissziós együtthatókat az
transzmissziós együtthatókat az
| (5.18) |
összefüggések szolgáltatják, ahol az s és p indexeket az egyszerűség végett elhagytuk, mert mindkettő esetén fennáll az összefüggés. A Fresnel-féle formulákat alkalmazva megmutatható, hogy
| (5.19) |
reláció teljesül, amely az energia megmaradását fejezi ki.
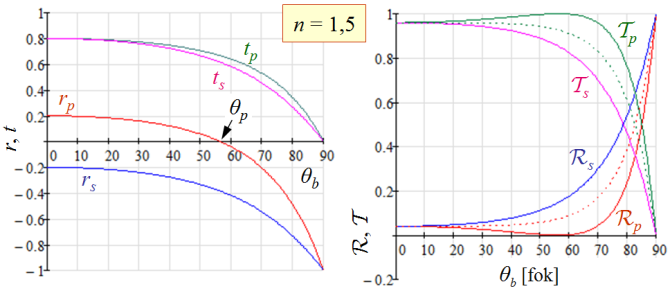 |
| 5.3. ábra. A Frensnel-féle formulából számolt amplitúdóra (balra) illetve a fényteljesítményre (jobbra) vonatkozó reflexiós és transzmissziós együtthatók n = 1,5 relatív törésmutató esetén. A fényteljesítmény esetén a pontozott vonal az s és p komponensekre vonatkozó átlagát mutatja, amely természetes fény esetén adja meg az adott együtthatókat. |
Az ábrán jól látható, hogy a θp-vel jelölt szög esetén a visszavert p összetevő amplitúdója zérus. Aminek a következtében ilyen beesési szög esetén a visszavert fény a beesési síkra merőleges irányú lineárisan poláros lesz. Ezért ezt a szöget polarizációs szögnek vagy Brewster-féle szögnek nevezzük. Az 5.17a összefüggésből következik, hogy rp = 0 ha
![]() ,
,
ami akkor tejesül, ha ![]() . Így a θb = θp beesési szöghöz tartozó törési szög θt = π/2 – θp. Ha erre az esetre alkalmazzuk a törés törvényét, akkor az
. Így a θb = θp beesési szöghöz tartozó törési szög θt = π/2 – θp. Ha erre az esetre alkalmazzuk a törés törvényét, akkor az
| (5.20) |
egyenletet kapjuk a polarizációs szögre.
Az n < 1 eset sok mindenben hasonlít az 5.3. ábrán szemléltetett n > 1 esethez, például az előbb ismertetett Brewster-féle törvénynek megfelelően a polarizációs szög alatt beeső fény visszaverődve a felületről lineárisan poláros lesz. Egy nagyon lényeges különbség van azonban a két eset között: a beesési szöget növelve, egy bizonyos határszög után az rp és rs reflexiós együtthatók komplex értéket vesznek fel. Mindkettőnek az abszolút értéke pontosan egységnyi lesz. Ennek következtében a felület egy tökéletesen visszaverő tükörként viselkedik. A továbbiakban ezzel az érdekes és nagyon fontos gyakorlati alkalmazásokkal bíró jelenséggel, a bevezetőben is már említett teljes visszaverődéssel foglalkozunk.