Kontinuitási egyenlet

Az M-1 egyenlet divergenciáját véve, valamint kihasználva, hogy egy vektortér rotációjának divergenciája azonosan zérus, vagyis itt , és az M-3 egyenletet felhasználva, az idő szerinti deriválást és a divergencia képzést felcserélve, az

(1.17)

formulát kapjuk, és amely kontinuitási egyenlet néven ismert, és a töltés megmaradását fejezi ki. Ugyanis, ha 1.17. egyenletet egy V térfogatra integráljuk és az áramsűrűség divergenciáját tartalmazó tagra alkalmazzuk Gauss-tételét, akkor

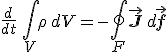összefüggéshez jutunk, ahol F a V térfogat felületét jelöli. Amit egy adott (t₀, t₁) időintervallumra integrálva a

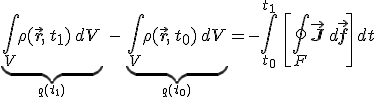(1.18)

egyenletre vezet. A bal oldalon a t₁ és a t₀ időpontban a V térfogatban lévő töltések különbsége, q(t₁) − q(t₀), míg a jobb oldalon a negatív jel után a tartomány felületén a (t₀, t₁) időintervallumban átáramló töltés áll. Az F felület azon pontjaiban, ahol J felületre merőleges komponense kifelé mutat, a töltések ki, míg ahol befelé mutat, a töltések beáramolnak a térfogatba. Vagyis ez utóbbi egyenlet pontosan azt fejezi ki, hogy egy tetszőleges V térfogatban az elektromos töltés pontosan akkora mennyiséggel csökken (vagy növekszik), mint amennyi töltés a térfogat felszínén kiáramlik (vagy beáramlik). Az elmondottak alapján 1.18. egyenlet a töltés globális, míg az 1.17. egyenlet pedig a lokális megmaradását fejezi ki.