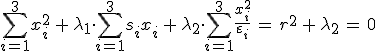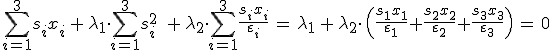A rezgési irányok geometriai meghatározása

A 11.16. és 11.17. egyenletek szerint az elektromos és mágneses tér energiasűrűsége megegyezik, ezért főtengely-rendszerben a

(11.44)

	11.4. ábra. Az index-ellipszoid perspektivikus ábrázolása  arány esetén.

egyenlet adja meg az energiasűrűséget. Ha az

(11.45)

definícióval új változókat vezetünk be, akkor ezekkel a 11.44. egyenlet az

(11.46)

alakba írható, amely egy ellipszoidnak, az ún. index-ellipszoidnak az egyenlete. Ez mellett több más elnevezés is használatban van: indikátrix, hullámnormális-ellipszoid vagy reciprok-elliszoid néven is szoktak hivatkozni rá. A 11.46. egyenletből látható, hogy az index-ellipszoid főtengelyei egybeesnek a főtengely-rendszer tengelyeivel, és a féltengelyek hosszát a fődielektromos állandók gyökei adják meg. Az index-ellipszoid segítségével egy adott s hullámnormálishoz tartozó két v_p fázissebesség és D elektromos eltolás két rezgési iránya szemléletesen meghatározható: Nevezetesen, az index- ellipszoid középpontján átmenő s-re merőleges síkkal kimetszett ellipszis főtengelyinek irányai megegyeznek D két rezgési irányával, továbbá a tengelyek hosszának reciprok értékei arányosak a két fázissebességgel. Az állítási igazolása céljából írjuk fel az s normálvektorú sík egyenletét:

.

(11.47)

Az index-ellipszoidnak a síkbeli metszete egy ellipszis, melynek pontjai egyszerre elégítik ki a 11.46. és 11.47. egyenleteket. Az ellipszis kis- és nagytengelye az átmérők közül a legkisebb, illetve a legnagyobb. Így ezek irányait egy feltételes szélsőérték feladat megoldásával határozhatjuk meg: keressük az

(11.48)

függvény minimumát illetve maximumát úgy, hogy az (x₁, x₂, x₃) pont a metszet ellipszisen van, amely azt jelenti, hogy teljesülnek a 11.46. és 11.47. egyenletek. A matematikai analízisből ismert, hogy a  Lagrange-féle multiplikátoros eljárással egy feltételes szélsőérték feladat visszavezethető egy megszorítás nélküli szélsőérték problémára. Ez alapján a 11.48. függvénynek a 11.46. és 11.47. egyenletek melletti (feltételes) szélsőértékei megegyeznek az

(11.49)

függvény (feltétel nélküli) szélsőértékeivel, ahol λ₁ és λ₂ a Langrange-multiplikátorok. A λ₁ előtti kettes tényezőt csupán - később érthető - kényelmi szempontok miatt vezettük be. Az F függvény szélsőértékének szükséges feltétele a parciális deriváltjainak eltűnése, azaz az i = 1, 2, 3 indexekre

.

(11.50)

A multiplikátorok szerinti parciális deriváltak eltűnése a mellékfeltételek miatt automatikusan teljesül. A 11.50. egyenletet az i = 1, 2, 3 indexekre x_i/2 értékkel beszorozva, és az egyenleteket összeadva az

(11.51)

összefüggéshez jutunk, ahol az első átalakításnál kihasználtuk a 11.46. és 11.47. mellékfeltételeket. Szorozzuk meg ismételten a 11.50. egyenletet az i = 1, 2, 3 indexekre ezúttal s_i/2 értékkel, és adjuk össze megint az egyenleteket. Így az

(11.52)

relációt nyerjük, ahol ismét kihasználtuk a 11.47. mellékfeltételt illetve az s vektor egységnyi hosszát. A 11.51. és 11.52. egyenletekből a multiplikátorok

és      ,

melyet visszahelyettesítve a 11.50. szélsőérték feltételbe az

(11.53)

egyenletrendszerhez jutunk (i = 1, 2, 3). A 11.44. és 11.45, valamint a 11.26, és a 11.8. egyenletek alapján az

,          és

összefüggések állnak fenn, melyekből a szélsőérték feltételét kifejező 11.53.  egyenlet az

alakot ölti. Ebből már egyszerű átrendezéssel az

	11.5. ábra. Az index-ellipszoid középpontján átmenő, az s hullámnormálisra merőleges síkmetszete ellipszis, melynek a tengelyeinek iránya azonos a D elektromos eltolás rezgési irányával. Az adott rezgési irányhoz tartozó fázissebesség fordítottan arányos a féltengely hosszával. Az animáción a hullámnormálist zöld, a féltengelyeket kék szín jelöli. ()

reláció adódik, amely megegyezik azzal a 11.31. egyenlettel, melyből a rezgési irányokra és fázissebességre vonatkozó megállapításokat származtattuk. Ez pedig pontosan azt jelenti, hogy a féltengelyek iránya az elektromos eltolás irányával megegyeznek, mert a 11.45. koordinátákkal definiált vektor a D elektromos eltolással azonos irányú. Ezzel az állítás első részét igazoltuk. Az eredményünket a 11.5. ábra szemlélteti. Mivel az ellipszis tengelyei merőlegesek egymásra, az elmondottakból következik a már említett állítás, hogy a két fázissebességhez tartozó két rezgési irány szintén egymásra merőleges. A fázissebességekre vonatkozó megállítás az és a összefüggésekből következnek:

,

(11.54)

ahol r_1,2 az ellipszismetszet féltengelyinek a hossza. Ebből már könnyen látható, hogy amennyiben a hullámnormális iránya valamelyik főtengely irányával azonos, akkor D a másik két főtengely irányában rezeg, és a két fázissebesség megegyezik a két főtengelyhez tartozó fősebességekkel, mivel a féltengelyek hosszát a fődielektromos állandók gyökei adják meg.

11.6. ábra. Általános esetben két, - a legkisebb és a legnagyobb fődielektromos állandókhoz tartozó tengelyek síkjában, az ábra síkjában fekvő, - irány van, melyekre merőleges síkkal elmetszve az index- ellipszoidot kör síkmetszetet kapunk. Ezeket sárga és barna szín jelöli az animáción. A sötét zöld színnel ábrázolt s hullámnormálishoz tartozó - világos zöld - ellipszis síkmetszeten, a körök és az ellipszis síkjának metszésvonalainak szögfelezői kijelölik az ellipszis tengelyinek irányát. ()

A s irányra merőleges síkmetszet ellipszis a féltengelyeinek az irányát, és így a rezgési irányokat geometriai eljárással szintén meghatározhatjuk. Általában  egy ellipszoid középpontján átmenő síkkal elmetszve ellipszist kapunk. Azonban mindig van kettő t₁ és t₂, - a legkisebb és a legnagyobb tengely a síkjában fekvő, - irány, amelyre merőleges síkmetszet kör lesz. Ez a két különleges irány jelöli ki a kristály optikai tengelyét. Ezek irányait barna nyíl jelöli a 11.6. ábrán látható animáción. A körmetszeteket sárga és barna, az ellipszis metszetet zöld szín szemlélteti.

A két körmetszet sugarának nyilvánvalóan azonosnak kell lenniük, mivel a középpontjuk egybeesik és a két körnek van közös pontja. A két körnek szintén van közös pontja az s irányhoz tartozó ellipszis síkmetszettel. Ezeket M₁ illetve M₂ jelöli a 11.7. ábrán. Mivel két kör sugara egyenlő, az OM₁ és az OM₂ szakaszok hossza is szükségképpen egyenlő. Ekkor viszont a két szakasz az ellipszis tengelyeire vonatkozólag csak szimmetrikusan helyezkedhet el. Így szükségképpen az ellipszis és a két kör síkjának metszésvonalainak a szögfelezői adják meg a rezgési irányokat, ahogy az a 11.7. ábrán is látható. Ezen az ábra (b) részén a hullámnormális irányából nézünk az index-ellipszoidra.

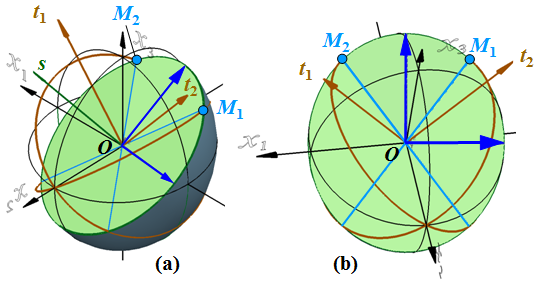11.7. ábra. Az elektromos eltolás rezgési irányait az és  szakaszok belső  illetve külső szögfelezője jelöli ki. Az ábra (b) részén az s hullámnormális irányából nézünk az index-ellipszoidra. A metszetet úgy forgattuk, hogy az ellipszis tengelyei vízszintesen illetve függőlegesen álljanak.

A két t₁ és t₂ irány különleges tulajdonsággal rendelkezik. Mivel az index-ellipszoid ehhez a két speciális irányhoz tartozó síkmetszete két azonos sugarú kör, melyre így a kis- és nagytengelyek egyenlők, a tengelyek hosszának szemléletes jelentése miatt (11.54. egyenlet), a t₁ és t₂ irányra a két polarizációs állapothoz tartozó két fázissebesség egyenlő. Vagyis az optikai tengelyek azokat az irányokat jelölik ki, melyekre a két polarizációs állapothoz tartozó fázissebességek azonosak. Mivel az ellipszoidnak bármely, ettől a két speciális iránytól különböző irányhoz tartozó síkmetszete körtől különböző ellipszis, a két optikai tengelytől eltérő irányokba a két fázissebesség különböző.

	11.8. ábra. Az elektromos eltolás a hullámnormális és az optikai tengelyek által kifeszített síkok és a ellipszis síkmetszet metszésvonalainak belső és külső szögfelelőinek irányába rezeg.

Az elektromos eltolás rezgési irányait meghatározhatjuk a hullámnormális és az optikai tengelyek által kifeszített (s, t₁) illetve (s, t₂) síkok segítségével is a 11.8. ábrán vázolt módon. Mivel az M₁ közös pontja az s-re merőleges ellipszisnek és a t₁-re merőleges körnek, az OM₁ szakasz egyaránt merőleges az s és t₁vektorokra. Ennek következtében az OM₁ szakasz az (s, t₁) sík normál vektora. Hasonló okok miatt az OM₂ szakasz az (s, t₂) sík normál vektora. Jelölje S₁ és S₂ az (s, t₁) illetve (s, t₂) síkoknak és az ellipszis metszetnek a 11.9. ábrán látható közös pontjait. Az elmondottak alapján az OS₁ szakasz az OM₁ szakaszra, míg az OS₂ szakasz az OM₂ szakaszra merőleges. Ennek megfelelően az OS₁ és OS₂ szakaszok - az OM₁ és OM₂ szakaszokhoz hasonlóan - szimmetrikusan helyezkednek el az ellipszis tengelyeire vonatkozólag. Így a rezgési irányokat az OS₁ és OS₂ szakaszok belső és külső szögfelezőinek irányaiból is megkaphatjuk, ahogy azt a 11.9. ábra szemlélteti. Az ábra (b) részén megint a hullámnormális irányából, vagyis merőlegesen tekintünk a metszet ellipszisre.

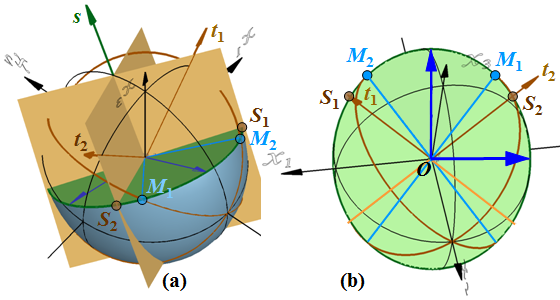11.9. ábra. Az elektromos eltolás rezgési irányait az  és  szakaszok belső  illetve külső szögfelezője jelöli ki. Az ábra (b) részén az s hullámnormális irányából, vagyis az ellipszis metszetre merőleges nézünk vissza. A metszetet megint úgy forgattuk, hogy az ellipszis tengelyei vízszintesen illetve függőlegesen álljanak, a 11.7. ábrához hasonlóan.

Az energiasűrűséget kifejezhetjük az elektromos térerősséggel is. A főtengely-rendszerben az 11.44. egyenlet az E térerősséget használva változóként a

(11.55)

alakot ölti. Ha bevezetjük az

(11.56)

változókat (i = 1, 2, 3), akkor a 11.55. egyenlet az

(11.57)

összefüggéssel ekvivalens, amely a 11.9. kvadratikus alak főtengely-rendszerbeli alakja. A 11.57. egyenlettel definiált ellipszoidot sugár-ellipszoidnak, vagy ahogy azt már említettük Fresnel-ellipszoidnak szokás nevezni. Könnyen ellenőrizhető, hogy a dualitás-szabályt alkalmazva az 11.45. összefüggés a 11.57. egyenletbe transzformálódik és megfordítva. Ez nyilván azt jelenti, hogy a sugár- és az index-ellipszoid egymás duálisai.

Ennek következtében az index-ellipszoid segítségével levont következtetések átvihetők a sugár-ellipszoidra vonatkozólag. Így a sugár-ellipszoid t sugárvektorra merőleges középponti síkmetszetével kapott ellipszis tengelyeinek iránya megadja az elektromos térerősség rezgési irányait, továbbá a két rezgési irányhoz tartozó két sugársebesség fordítva arányos az ellipszis kis- és nagy féltengelyeinek hosszával. Mivel az ellipszis tengelyei egymásra merőlegesek, a térerősség két rezgési iránya szintén merőlegesek.

A 11.57. egyenletből látható, hogy a sugár-ellipszoidnak a féltengelyeinek hossza az index-ellipszoid féltengelyei hosszának a reciprok értéke. Ennek megfelelően a legnagyobb és a legkisebb tengelyek szerepet cserélnek. Most is létezik kettő, és csakis kettő, olyan irány melyre merőleges központi síkmetszet kör. Ezek az irányok definiálják a sugártengelyeket. Ezekre az irányokra, és csakis ezekre, a két egymásra merőleges E rezgési irányhoz tartozó két sugársebesség megegyezik. A két sugártengely (az optikai tengelyekhez hasonlóan) a legkisebb és a legnagyobb féltengelyek által kifeszített síkban vannak. A két ellipszoid legkisebb és legnagyobb tengelyeinek reciprok kapcsolata  miatt a sugártengelyek és az optikai tengelyek közös síkban vannak.