Polarizációs tulajdonságok
Polarizációs ellipszis
A 3.15. egyenletekből az elektromos térerősséget az
| (3.18) |
alakban írhatjuk fel, ahol
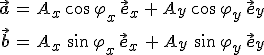 . . |
(3.19) |
Ebből kiindulva a monokromatikus vektorhullámok polarizációjáról elmondottakat közvetlenül alkalmazhatjuk. Egyszerűen beláthatók a következő összefüggések:
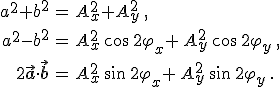 |
(3.20) |
Ezeket a 2.52. egyenletbe helyettesítve és a trigonometrikus azonosságokat felhasználva, az ellipszis féltengelyeinek a hosszára
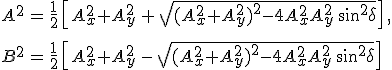 |
(3.21a-b) |
adódik, ahol δ = φx − φy = αy − αx a két komponens közötti fáziskülönbség. A 3.21 egyenleteit összeadva, valamint az elsőből a másodikat kivonva és négyzetre emelve, egyszerű számolással az
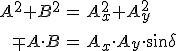 |
(3.22a-b) |
formulákat nyerjük.
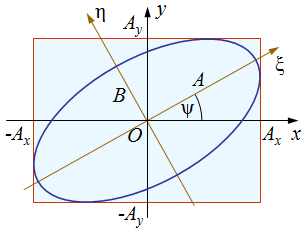 |
|
| 3.1. ábra. A polarizációs ellipszis. |
A 2.50. és a 3.20. egyenletekből következik, hogy
| (3.23) |
Ebből megmutatható, hogy
| (3.24) |
Így - a polarizáltság irányáról elmondottak szerint - balra elliptikusan poláros esetben B iránya az η tengellyel egyező, míg jobbra elliptikusan poláros esetben ellentétes irányú. Ezért a 2.46. egyenlet alapján a 3.1. ábrán ábrázolt polarizációs ellipszis tengelyeinek az irányában álló (ξ, η) koordináta-rendszerben
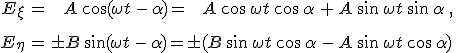 , , |
(3.25a-b) |
ahol a felső előjel a balra, míg az alsó előjel a jobbra polaritás irányra vonatkozik. Határozzuk meg a 3.1. ábrán ábrázolt polarizációs ellipszis helyzetét megtározó ψ szöget! Jegyezzük meg, hogy a 2.54. egyenlettel adott szöget - eltérően a mostani jelöléstől - az a vektortól mértük. Azonban alkalmazásoknál célszerűbb lehet egy szabadon választott iránytól (mondjuk az x tengelytől) is meghatározni a helyzetet megadó szöget. Az E vektor (x, y) koordináta-rendszerbeli és a ψ szöggel elforgatott (ξ, η) koordináta-rendszerbeli koordinátáit az
| (3.26a-b) |
forgatási transzformáció köti össze. A 3.15. egyenletekből a térerősség komponenseit behelyettesítve és a cos függvény addíciós képletét felhasználva, továbbá a a 3.25. egyenlettel összevetve, és a cos ωt és sin ωt együtthatóit egyenlővé téve a következő egyenlethez jutunk:
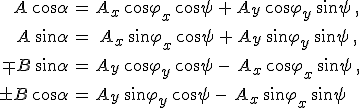 . . |
(3.27a-d) |
Az előző egyenletekből az első és a harmadik, valamint a második és a negyedik szorzata egy előjelben különbözik csak. Ez egy egyenletet szolgáltat a keresett ψ szögre, amely a trigonometrikus azonosságok többszöri alkalmazásával a
| (3.28) |
eredményt adja. A 3.27. egyenletekből szintén megkaphatók a 3.22. összefüggések. Ha az egyenletek négyzeteit összeadjuk és a trigonometrikus azonosságokat alkalmazzuk, akkor 3.22a formulát kapjuk. Hasonlóan a 3.27. második és harmadik egyenletének szorzatából kivonva az első és a negyedik szorzatát, trigonometrikus átalakításokkal 3.22b képlethez jutunk, melyben a felső előjel vonatkozik balra, míg az alsó előjel jobbra polarizált esetre.
Az egyenletek egyszerűbb alakba történő írása végett célszerű bevezetni a
| (3.29a-b) |
definíciókkal a 0 ≤ β < π/2 és a -π/4 ≤ χ ≤ π/4 segédszögeket. Látható, hogy χ szög nagysága az ellipszis lapultságára jellemző. Előjelével kapcsoltban, megállapodás szerint negatív illetve pozitív a balra illetve jobbra polarizált fényre vonatkozólag. A β segédszöggel, a ![]() összefüggést felhasználva, a 3.28. egyenlet a
összefüggést felhasználva, a 3.28. egyenlet a
| (3.30) |
alakba írható át. A 3.22. második összefüggését 2-vel szorozva és az elsővel elosztva
|
|
(3.31) |
adódik, ahol a jobb oldalon 3.29b egyenlettel definiált χ szöggel fejeztük ki. Hasonló módon a bal oldalt 3.29a egyenlettel értelmezett β szöggel átalakítva
| (3.32) |
formulához juthatunk.