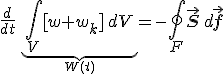Az energia terjedése. Intenzitás

Ha egy elektromágneses térben egy q töltésű, m tömegű részecske tartózkodik, akkor a rá az Lorentz-féle erő hat, és a mozgását az mozgásegyenlet határozza meg, amit - mivel az anyag folytonos eloszlású - célszerű a

differenciális alakba felírni, ahol v a részecske sebessége, ρ_m a tömeg-, ρ a töltéssűrűség, J = ρv az áramsűrűség, E az elektromos térerősség, B a mágneses indukció. Az 1.17. egyenletet a sebességgel skalárisan megszorozva, egyszerű átalakítással az

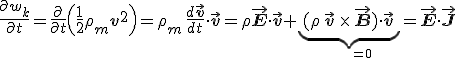(1.19)

egyenletet kapjuk, ahol w_k a kinetikai energia sűrűsége. Az M-1 egyenletet E-vel, az M-2 egyenletet H-val skalárisan szorozva az

	(1.20a)
	(1.20b)

képletekhez jutunk. Az 1.20b egyenletből az 1.20a egyenletet kivonva, valamint az 1.19. egyenletet és a azonosságot alkalmazva az

(1.21)

összefüggés adódik. Az 1.3. és 1.7. lineáris anyagegyenletek fennállta esetén 

     és az   

teljesülnek. Így az 1.19. egyenletet is figyelembe véve, 1.21. egyenletet az

(1.22)

alakra hozhatjuk, ahol

(1.23)

az úgy nevezett Poynting-féle vektor és

(1.24)

az elektromágneses mező energiasűrűségeként értelmezhető. Ugyanis az 1.22. egyenlet formailag teljesen megegyezik a töltés-megmaradást kifejező kontinuitási egyenlettel, és így töltés megmaradásához hasonlóan, az energiamegmaradását fejezi ki lokális alakban. Most is az 1.22. egyenletet egy adott V térfogatra integrálva és Gauss-tételével a divergenciát tartalmazó tagot tartomány felületére vonatkozó integrálra átírva

(1.25)

összefüggéshez jutunk, ahol F a V térfogat felületét jelöli. A bal oldalon lévő integrál a t időpontban a V térfogatban lévő energiát adja meg, amely két tagból az elektromágneses mező energiájából és a töltött anyag mozgási energiájából tevődik össze. Ebből az egyenletből kiolvasható a Pointing-vektor jelentése: a felület kicsiny Δf nagyságú felületén kicsiny Δt idő alatt ΔW = S·n·Δf·Δt energia áramlik keresztül, ahol n a kifelé mutató felületre merőleges egységvektor. Ahol S felületre merőleges komponense kifelé mutat, az energia áramlik ki, míg ahol befelé mutat, az energia áramlik be a térfogatba. Azaz S az elektromágneses tér energiaáramlás-sűrűsége. Az 1.25. egyenletet egy adott (t₀, t₁) időintervallumra integrálva a

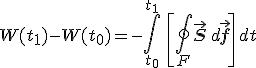(1.26)

 egyenlethez jutunk. A bal oldalon a t₁ és a t₀ időpontban a V térfogatban lévő energia különbsége, míg a jobb oldalon a negatív jel után a térfogat felületén a (t₀, t₁) időintervallumban átáramló energia áll. Ily módon az 1.25. és 1.26. egyenletek az energia megmaradását fejezik ki globális formában.