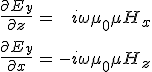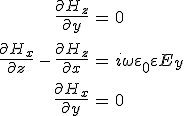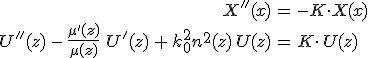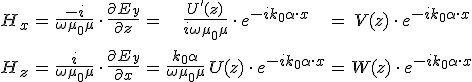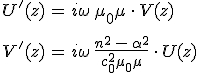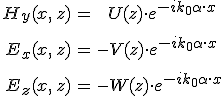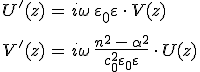Hullámok rétegezett közegben

Tekintsünk egy monokromatikus elektromágneses síkhullámot, és vizsgáljuk meg, hogy hogyan halad keresztül egy rétegezett közegen. A beeső hullám terjedési iránya és a rétegződés irányát megadó z tengely együtt meghatározza a beesési síkot. A Frensel-formulák esetében alkalmazott vonatkoztatási rendszert fogjuk használni, azaz a koordináta-rendszert úgy választjuk meg, hogy a beesési sík legyen az (x, z) sík. Az elektromos térerősséget most is célszerű felbontani két komponensre, a beesési síkra merőleges s, illetve a beesési síkkal párhuzamos p komponensekre. Azt az elektromágneses hullámot, melynek az elektromos térerőssége merőleges a beesési síkra s-polarizált míg amelynek a térerőssége párhuzamos a beesési síkkal p-polarizált hullámnak nevezzük. Ha egy s-polarizált hullámot tekintünk, azaz , akkor az M2-egyenletből és az 1.7. anyagegyenletből, monokromatikus hullámnál exp[iωt] időfüggést feltételezve,

(6.2)

következik, amiből rögtön látható, hogy H_y = 0. Azaz egy s-polarizált monokromatikus hullámra alakú a mágneses térerősség. Hasonlóan megmutatható hogy, az 1.3. anyagegyenletből és az M1-egyenletből (J = 0 mellett) következik, hogy esetén

(6.3)

áll fenn, amiből pedig következik, azaz az ilyen hullám p-polarizált. Mivel s-polarizált hullámra az elektromos, az p-polarizált hullámra a mágneses térerősség merőleges a beesési síkra az s és p jelölések helyett szokásos még E- és H-polarizált, vagy TE és TM elnevezések használata is. A Maxwell-egyenletekből következik, hogy az s- és p-polarizált hullámok egymástól függetlenül terjednek, amint azt már az előző fejezetben is láttuk a törés és visszaverődés vizsgálatánál. Itt láttuk, hogy az optikai tulajdonságok ugrásszerű változása esetén az s és p komponensekre vonatkozó peremfeltételek egymástól függetlenek. Az elmondottak szerint s-polarizált hullám esetén a térerősségeket derékszögű koordinátákkal az

és

(6.4)

alakba írhatjuk, míg egy p-polarizált hullámra

és

(6.5)

adja meg az elektromos és mágneses térerősséget. Ezek a formulák azt mutatják, hogy bármely beeső monokromatikus hullámot könnyen felbonthatunk s- és p-polarizált hullámok összegére.

Az s- és p-polarizált hullámokra való felbontásnak másik előnye, hogy a számolásokat elegendő az egyikre, mondjuk az s-polarizál hullámra elvégezni, mert a másikra vonatkozó eredményt ebből már egyszerű változó cserével megkaphatjuk. Ugyanis, nem-elnyelő izotrop közeg esetén (azaz makroszkopikus töltések és áramok hiányában) a Maxwell-egyenletek invariánsak az    és    egyidejű változó cserére. Így az H-polarizált hullámra vonatkozó egyenlet megoldását, az E-polarizáltra vonatkozó megoldásból megkaphatjuk az előbbi cserével.

Vizsgáljuk meg, hogy a 6.4. alakú térerősségekkel adott s-polarizált hullám hogyan terjed egy rétegzett közegben. A 6.2. vektor egyenletet derékszögű koordinátákkal kifejezve az

(6.6)

összefüggésekhez jutunk, ahol a H_y = 0 egyenletet már nem írtuk ki. Az 1.3. és az M1-egyenletből (J = 0 feltételt figyelembe véve) pedig a

(6.7)

egyenletek adódnak. Látható, hogy H_x és H_z komponensek y szerinti parciális deriváltjaik nullák, ami azt mutatja, ezek függetlenek az y koordinátától, azaz

és       .

(6.8)

Amiből a 6.7. középső egyenlete miatt E_y szintén csak ezen változók függvénye, azaz

.

(6.9)

Ha 6.6. egyenletekből kiszámoljuk a mágneses térerősség 6.7. középső egyenletbeli parciális deriváltjait és ezeket behelyettesítjük az egyenletbe, akkor egyszerű számolással a

(6.10)

egyenletet kapjuk, ahol k₀ = ω/c₀ vákuumbeli körhullámszám, a törésmutató. Keressük az egyenletünk megoldását

(6.11)

alakban, azaz a változók szeparálásával próbáljuk megoldani a terjedést leíró alapegyenletet. Ha ezt az előállítást a 6.10. egyenletbe helyettesítjük, akkor változó szeparálásnál szokásos módon az egyenletet olyan alakra hozhatjuk, hogy az egyik oldala csak x, míg a másik oldala csak a z változó függvénye. Ez nyilván csak úgy lehetséges, ha a két oldalon lévő kifejezés egy állandó, melyet K jelöl majd. Az elmondottakat követve beláthatjuk, hogy a szorzótényezőkre az

(6.12)

összefüggéseket érvényes, ahol a szeparációs állandót érdemes egy szám négyzetének tekinteni, így a

(6.13)

alakba írjuk fel. Az α állandó fizikai jelentését később tisztázzuk. A 6.12. első egyenletének egy megoldása, ahol C egy állandó. Ha ezt visszahelyettesítjük a 6.11. elállításba, akkor az

(6.14)

összefüggés kapjuk az elektromos térerősségre, ahol az X tényezőben lévő C szorzót belefoglaltuk az U(z) függvénybe. A 6.6. és a 6.14. egyenletekből a

(6.15)

képletek adódnak a mágneses térerősségre, ahol

és

(6.16)

függvények a mágneses térerősség komponensek z koordinátától függő tényezőit jelölik. Ezek nem függetlenek egymástól, mert 6.7. középső egyenlet miatt a

(6.17)

reláció áll fenn közöttük. A 6.16. és 6.17. egyenletekből a W(z) ismeretlen függvényt kiküszöbölve az

(6.18)

elsőrendű differenciál-egyenletrendszerhez jutunk, amelyről könnyen megmutatható, hogy ekvivalens 6.12. második egyenletével.

Ha az U komplex függvényt az

(6.19)

exponenciális alakban írjuk fel, akkor a 6.14. egyenlet szerint A(z) adja meg az elektromos térerősség amplitúdóját, továbbá

(6.20)

az elektromos térerősség fázisa.  Ami alapján látható, hogy az állandó amplitúdójú felületek - melyek a z tengelyre merőleges síkok - különböznek az állandó fázisú felületektől. Vagyis a rétegezett közegben inhomogén hullám terjed. Az azonos fázisú felületek általános esetben görbült felületek. melyeknek egy adott helyen a felületi normálisának a z tengellyel bezárt szögét a 6.20. egyenletből számolhatjuk ki. A felületi normális a gradiens irányába mutat, ezért a felületi normálisnak a z tengellyel bezárt θ szögét

(6.21)

összefüggés adja meg. Ha a hullám homogén síkhullám, akkor A állandó, valamint és . Így a 6.13. egyenletből következő

(6.22)

reláció a Snellius-Descartes-féle törvény rétegezett közegre vonatkozó általánosításának tekinthetjük.

A p-polarizált hullám terjedését leíró egyenleteket a már említett változó cserével rögtön megkaphatjuk. Ez alapján a nullától különböző térerősségeket a

(6.23)

alakban adhatjuk meg, ahol a z koordinátától való függést leíró U és V függvényeket

(6.24)

elsőrendű differenciál-egyenletrendszer megoldása szolgáltatja, továbbá

.

(6.25)