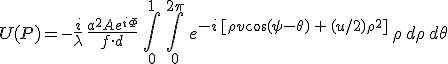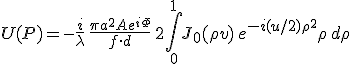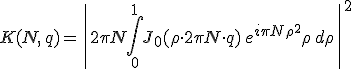Fresnel-elhajlás környíláson

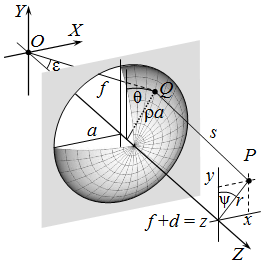
	10.21. ábra. Környíláson való Fresnel-elhajlás leírásánál használt koordináta-rendszer.

A továbbiakban az alkalmazásoknál is igen gyakori, ezért jelentős speciális esettel, egy a sugarú környílással foglalkozunk. Tegyük fel, hogy a forrás a környílás szimmetriatengelyén helyezkedik el és helyezzük ebbe a pontba a koordináta-rendszerünk origóját. Jelölje f a nyílást kitöltő hullámfront görbületi sugarát. Keressük a nyílás mögötti térerősséget z = f + d síkban lévő P pontban. A probléma hengerszimmetriája miatt célszerű a számolást hengerkoordináta-rendszerben elvégezni. A szokásos hengerkoordinátáktól annyiban térünk el, hogy a θ és ψ azimut-szögeket az Y tengelytől mérjük az X tengely helyett, ahogy az a 10.21. ábrán látható. A hullámfront általános Q pontjának radiális koordinátáját célszerű ρ·a alakban felírni, ahol 0 ≤ ρ ≤ 1. A 10.24. diffrakciós integrálból kiindulva, a Fresnel-féle elhajlásnál szokásos módon a távolságokat másodrendig közelítve, a számolás részletezése nélkül, a térerősséget az 

(10.86)

kifejezés adja meg, ahol

és

(10.87)

dimenziómentes változók, továbbá

.

(10.88)

A Fraunhofer-féle elhajlásnál látott módon, a 10.53. egyenlethez hasonlóan, az azimut-szög szerinti integrálást a J₀ Bessel-függvénnyel fejezhetjük ki, így 10.86. összefüggés az

(10.89)

alakba alakítható át. A 10.89. egyenletbeli integrált numerikus integrálással is kiszámíthatjuk, azonban a J_n(x) Bessel-függvények, a sin(x) és cos(x) függvények deriválásra vonatkozó tulajdonságait felhasználva, parciális integrálásokkal gyorsan konvergáló függvény-sorok alakjában lehet felírni, melyek a gyors konvergencia miatt különösen alkalmasak numerikus számolásra [1]. Ezzel az eljárással az integrált a kétváltozós Lommel-függvényekkel számíthatjuk ki [1].

A 10.89. egyenletből adódó elhajlási kép jellemzésére célszerű bevezetni az

(10.90)

egyenlettel definiált Fresnel-féle számot, melynek a segítségével az 10.87. első egyenletében megadott változó az

(10.91)

alakba írható. A Fresnel-szám szemléletes jelentéssel bír: azt mutatja meg, hogy a tengelyen lévő P pontból a nyílást kitöltő hullámfelület hány ún. Fresnel-féle zónára osztható fel. A zóna szerkesztést a 10.22. ábra szemlélteti. A zónák segítségével a diffrakciós integrál eredményét közelítőleg kiszámíthatjuk, és így a belőle következő eredményt szemléletesen értelmezhetjük.

10.22. ábra. A nyílást kitöltő hullámfront Fresnel-féle zónákra osztása. A tengelyen lévő P megfigyelési pontból R = d + m·λ/2 sugarú gömbökkel felosztjuk zónákra (m = 1, 2, 3, …). Megmutatható, hogy a zónák felülete egyenlő, így a szomszédos zónák a P pontban azonos nagyságú, de ellentétes fázisú rezgést létesítenek.

A zóna szerkesztés során a P pontból R = d + m·λ/2 sugarú gömbökkel zónákra osztjuk fel a hullámfelületet (m = 1, 2, 3, …). Megmutatható, hogy az így kapott zónák felülete közel azonos. Ezért mivel a szomszédos zónák közötti útkülönbség λ/2, Hugens-Fresnel-féle elv alapján két szomszédos zóna azonos nagyságú, de ellentétes fázisban lévő rezgést kelt a P pontban. Ennek megfelelően szemléletesen azt várjuk, hogy páros N esetén P pontban sötét, míg páratlan N esetén maximálisan világos lesz. A diffrakciós integrálból kapott számolás ezt a szemléletből kapott eredményt valóban megerősíti: A nyílás mögött megfigyelhető diffrakciós képet a 10.23. ábrán látható animáció mutatja, amely során az N Fresnel-féle szám változik.

10.23. ábra. Környílás mögött megfigyelhető elhajlási kép. Az animáció során az N Fresnel-szám változik. Figyeljük meg, hogy páros N esetén a tengelyen sötét, míg páratlan esetén maximálisan világos hely van. A vízszintes tengelyen ábrázolt mennyiség az r radiális távolsággal arányos, a geometriai árnyék határának ±1 felel meg. A függőleges tengelyen ábrázolt mennyiség azt mutatja meg, hogy az intenzitás hányszorosa a nyílás nélküli, zavartalan terjedéshez tartozó intenzitásnak.

A 10.87. egyenletekből következik, hogy a geometriai árnyék határán teljesül. A reláció a geometriai optika szempontjából a megvilágított tartománynak, a  egyenlőtlenség az árnyék tartományban teljesülnek. Érdemes a dimenziómentes változót a

(10.92)

alakba felírni. Az szerint, hogy P pont a geometriai optikai értelemben a megvilágított tartományban vagy az árnyék határán illetve az árnyékban van, sorrendben 0 ≤ q < 1 vagy q = 1 illetve q > 1 teljesül. Az N Fresnel-szám és a q változó segítségével, a 10.89. egyenlet alapján, a P pontbeli intenzitás

(10.93)

alakba írható fel, ahol

(10.94)

és

(10.95)

a nyílás nélküli zavartalan terjedéshez tartozó intenzitás. Látható, hogy a 10.94. kifejezéssel megadott tényező azt mutatja meg, hogy az elhajlás következtében a P pontban létrejövő intenzitás hányszorosa a zavartalan terjedéshez tartozó intenzitásnak. A 10.23. ábrán látható grafikon vízszintes tengelyén (tükrözve a negatív tartományra) a q paraméter, a függőleges tengelyén a K függvény értékeit ábrázoltuk. Látható, hogy maximális erősítés esetén a zavartalan terjedéshez tartozó intenzitás négyszeresét kapjuk. Ez összhangban van az elemi úton, a zónák segítségével származtatott megállapítással, mely szerint a zavartalan terjedéshez tartozó térerősség olyan mintha az első zóna fele hozná létre. Maximális erősítés esetén egy kompenzálatlan teljes zóna hatása érvényesül. Ennek megfelelően az intenzitások között négyszeres szorzó van.

Érdemes megjegyezni, hogy az alkalmazásoknál szintén különösen fontos környíláson áthaladó és elhajló konvergens gömbhullám formailag megegyező egyenletekkel tárgyalható. Ekkor az origó a beeső hullámfront görbületi középpontjában, a fókuszpontban (vagy általánosabban a képpontban) van. A konvergens gömbhullámra a 10.86. egyenlettel azonos összefüggés érvényes [1, 8], csak a 10.87. és 10.88. kifejezésekben az f mennyiség helyére –f értéket kell helyettesíteni. Megemlítjük még, hogy a formalizmus átvihető a lézernyalábok leírásnál fontos ún. Gauss-nyalábok környíláson történő elhajlásának tárgyalására is azzal a változtatással, hogy az u valós paraméter helyett egy komplex paramétert vezetünk be [9].