Várható érték becslése ismert szórás esetén

Tegyük fel, hogy  ahol  ismert, ismeretlen.

Legyen  statisztikai minta változóra.

Ezen minta alapján szerkesszük meg azt az intervallumot mely valamely kicsiny –általában 10% alatti –  p értékre 1-p valószínűséggel tartalmazza az  változó várható értékét.

A konfidencia intervallum alapgondolata az, hogy egy mintaátlag középpontú szimmetrikus intervallumot szerkesztünk, melynek sugarát a minta elemeinek eloszlásparaméterei alapján számoljuk.

A minta eloszlásra igaz, hogy:  .

Ekkor az:

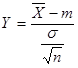
valószínűségi változó standard normális eloszlású változó.

Ebből kiindulva keressük azt az  sugarú intervallumot, melyre  melyre

Mivel a sűrűségfüggvény harmadik tulajdonsága alapján:

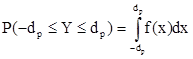
azaz azt szemléltetve a standard normális eloszlás sűrűségfüggvényével olyan intervallumot keresünk melyre a  intervallumon a sűrűségfüggvény alatti terület 1-p.

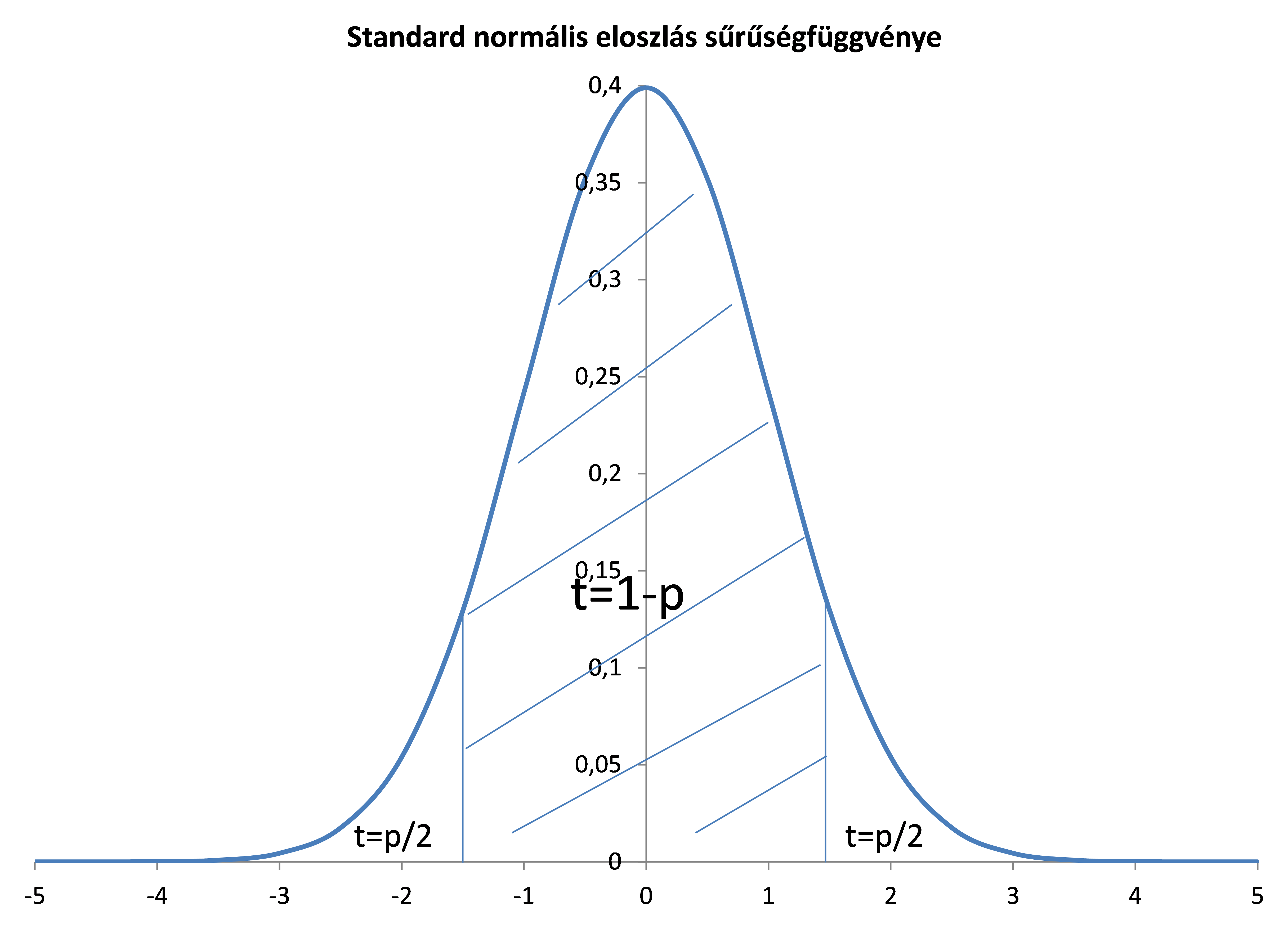
Mivel az eloszlás és sűrűségfüggvény viszonyára , így a Newton-Leibnitz szabályt alkalmazva:

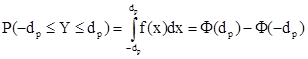
Azaz az eloszlásfüggvény függvényértékek közötti különbséggel méri egy esemény valószínűségét amit a sűrűségfüggvény függvény alatti területtel.

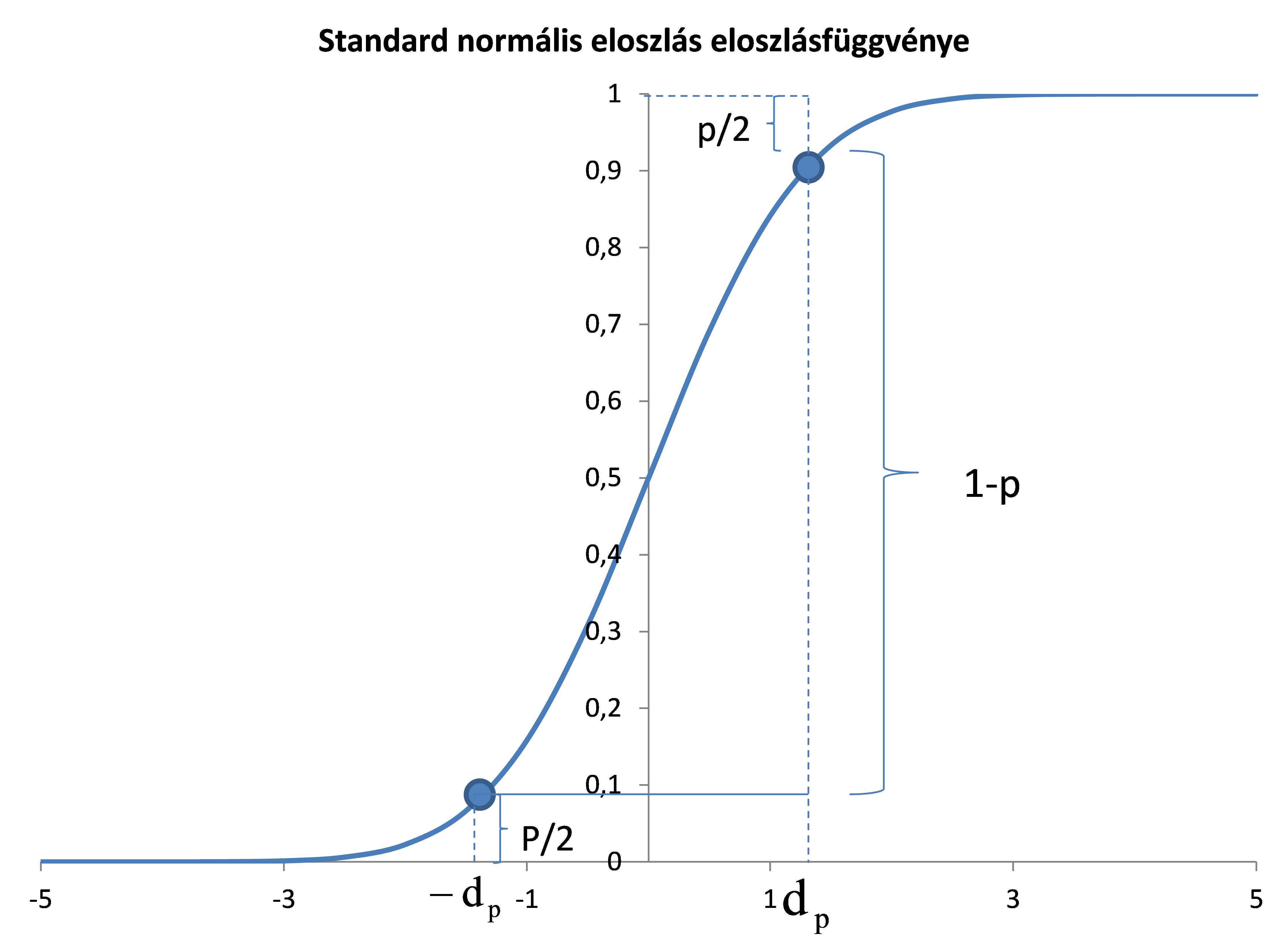
 Standard normális eloszlás eloszlásfüggvényére említettük hogy igaz az alábbi összefüggés a  pontra tükrös helyzet miatt:

azaz:

ahonnan:

Így

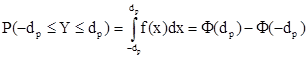
Beírva ezt a kiinduló összefüggésbe:

Felhasználva az eloszlásfüggvény középpontosan szimmetrikus helyzetéből kapott összefüggést:

Ekkor tehát :

behelyettesítve a definíciót

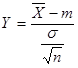
kapjuk, hogy:

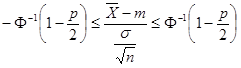
ahonnan az alábbi lépések következnek:

Innen -1-gyel szorozva kapjuk:

Innen a konfidencia intervallum:

Így megszerkeszthető az átlag körüli konfidencia intervallum, melynek sugara:

Ez az intervallum tartalmazza 1-p valószínűséggel az változó várható értékét.

Ha egy előírt megbízhatósági szinthez felső korlátot akarunk adni az intervallum sugarára akkor ha ez a korlát k akkor a következő egyenlőtlenséget kapjuk:

átrendezve:

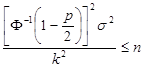
vagyis legalább ekkora minta elemszám szükséges a paraméter kielégítő becsléséhez.

Ha például p = 0,05 akkor  a következő statisztikai függvénnyel számítható Excelben: NORM.INVERZ(0,975;0;1).

Ennek értéke 1,959964.

Ekkor ha  és tudjuk, hogy a mintaátlag ,  a minta elemszáma pedig , akkor  az  megbízhatóságú konfidencia intervallum a következőképp számolható a konfidencia intervallum  fent felírt formulája alapján:

vagy a konfidencia intervallum sugarát megadó MEGBÍZHATÓSÁG statisztikai függvénnyel: