A valószínűség fogalma
A valószínűség axiomatikus megalapozásához a relatív gyakoriság tulajdonságaiból indulunk ki.
Definíció: Ha n független kisérletet végzünk egy 
esemény megfigyelésére és 
-szor következett be akkor -t az esemény gyakoriságának, a 
értéket pedig relatív gyakoriságának nevezzük és 
-val jelöljük.
A relatív gyakoriságra könnyen ellenőrizhető, hogy igazak a következők:
1. 
2. Ha I a biztos esemény akkor 
és 
kizáró események akkor 
.
Ez utóbbit könnyen igazolhatjuk véges sok eseményből álló halmazra is, akkor azt kell feltennünk, hogy páronként kizáró eseményeink vannak.
A valószínűség axiomatikus megalapozásakor a fenti tulajdonságokból mint axiómákból indulunk ki:
- Axióma Egy eseményalgebra minden 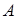eleméhez hozzá van rendelve egy
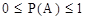szám, amely az 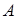esemény valószínűsége. - Axióma 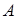biztos esemény valószínűsége 1, azaz
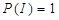. - Axióma
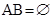esetén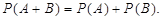 
- Axióma Ha
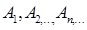egymást páronként kizáró események, akkor
A 3.axiómát véges sok eseményből álló halmazra is felírhatjuk a relatív gyakorisághoz hasonlóan, azzal a feltevéssel , hogy hogy páronként kizáró eseményeink vannak.