Korreláció kovariancia

Korrelációs együttható:

Legyen  valószínűségi változó várható értéke M(X) szórása D(X).

Legyen  valószínűségi változó várható értéke M(Y) szórása D(Y).

A két változó kovarianciáját az alábbi módon számítjuk:

Két változó közötti korrelációs együttható a következőképp számítható a kovariancia segítségével:

A korrelációs együtthatóra a következő összefüggések igazak.

.

Ha   és  változók függetlenek akkor 

Ezt úgy tudjuk igazolni, hogy kihasználjuk a függetlenség esetén fennálló

összefüggést, így igazolni tudjuk, hogy ekkor a két változó kovarianciája 0.

A két változó között determinisztikus lineáris kapcsolat van  vagy  esetén. Ha negatív a korrelációs együttható akkor negatív korrelációról beszélünk pozitív korrelációs együttható esetén pozitív korrelációról.

A két változó kapcsolatának szorosságát az jelzi ha a korrelációs együttható abszolút értéke 1-hez közeli.

Lineáris kapcsolat azt jelenti hogy vannak olyan  konstansok melyekre

Korrelációs együttható becslése.

Legyen

az  változóhoz tartozó minták 

 az  változóhoz tartozó minták .

Ebből a két mintából alkossuk meg a mintára vonatkozó korrelációs együtthatót.

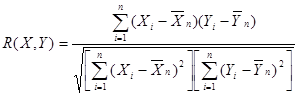
A korrelációs együttható becslése t.próbával történik.

Legyenek hipotéziseink a következők:

A minta korrelációs együtthatójából megalkotjuk a következő statisztikát:

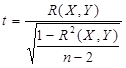
Ha a nullhipotézis igaz, ez a statisztika n-2 szabadságfokú t-eloszlású változó.

Excelben a korrelációt és kovarianciát a KORREL illetve a KOVARINCIA.M és KOVARIANCIA.S függvényekkel számíthatjuk.