Egymintás u-próba

Egymintás u-próba esetén ismert szórású normális eloszlású változó várható értékére végzünk hipotézisvizsgálatot .

Szemléltessük az alábbi példán a fenti gondolatmenetet.

Egy versenyző azt állítja, hogy tudja teljesíteni a versenyen való nevezéshez a 100 m-es síkfutásban a 12 másodperces szintidőt.

Az alábbi eredményeket mérték :

Ez alapján elfogadható-e a versenyző azon állítása, hogy teljesíti a szintet?

Tegyük fel, hogy tanuló futási teljesítményideje normális eloszlású, 1,5 sec szórású változó.

.

Amit ellenőrizni akarunk az az. hogy igaz-e a tanuló állítása hogy teljesíti a nevezéshez szükséges szintidőt.

Legyen  ahogyan a versenyző állítja.

Legyen ezért a nullhipotézis az, hogy:

Emellett fogalmazzuk meg az alternatív (vagy ellen) hipotézist:

 megengedett elsőfajú hibavalószínűség mellett döntsük el, hogy igazat mond-e a versenyző.

A fentebbi logikai menet alapján járunk el.

Ha igaz a nullhipotézis akkor :

.

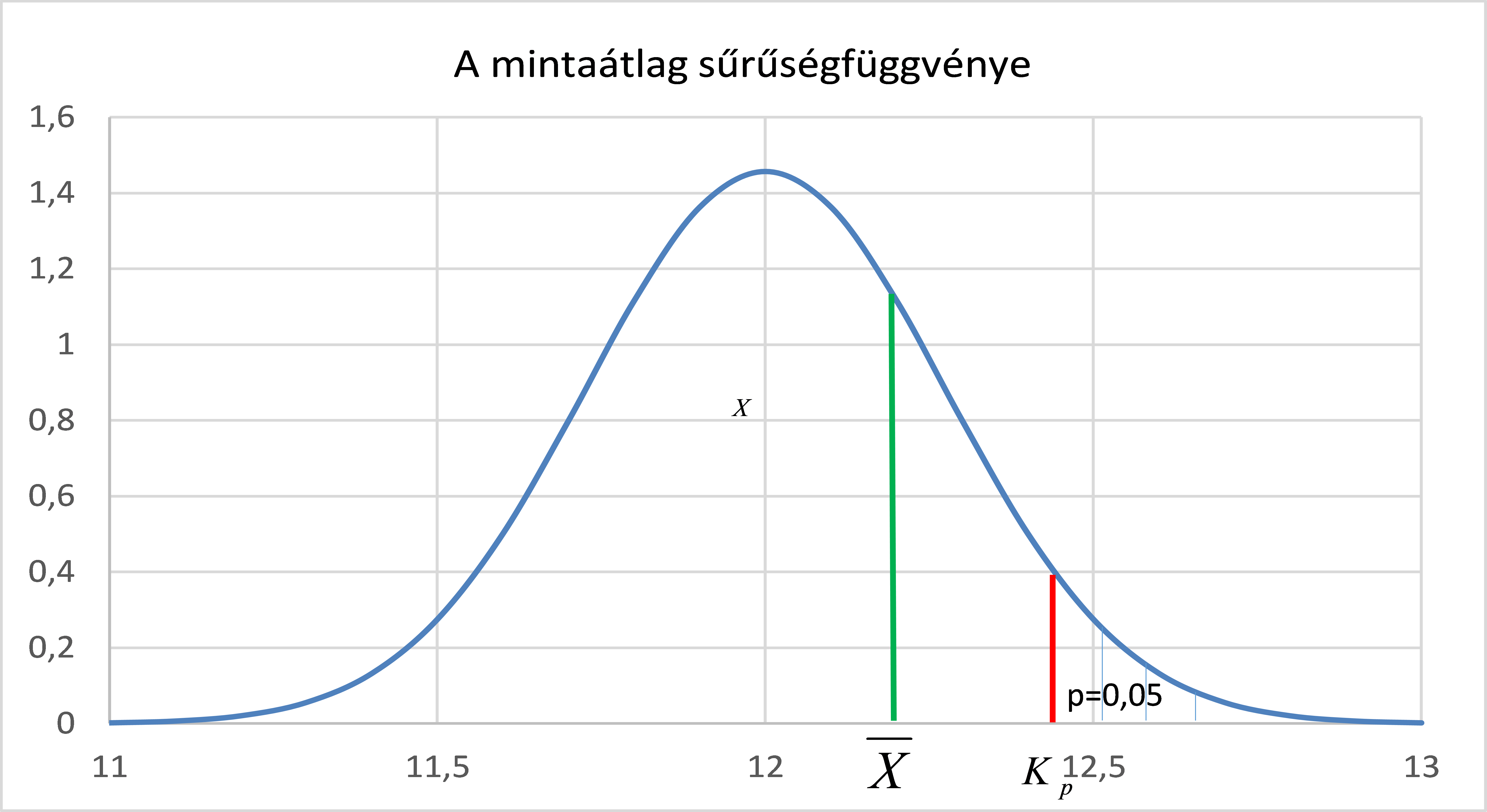
A kritikus érték meghatározása és a hipotézisvizsgálat a fentebb leírt logikai menet alapján a következőképpen folytatódik.

A mintaátlag tehát egy olyan normális eloszlású valószínűségi változó melynek várható értéke a nullhipotézis igaz logikai értéke esetén 12, szórása  .

Ha a mintaátlag egy konkrét mért minta esetén nagyobb mint a 12 akkor ezt két részhatás eredményének tulajdoníthatjuk:

• Egyrészt egy véletlen hatás eredményének, a mintavétel véletlen jellege miatt
• Másrészt azon hatás eredményének, hogy tanuló átlagos futóteljesítménye nem

12 sec/100 m hanem annál rosszabb.

Hogy ezek közül melyiket vesszük figyelembe azt úgy döntjük el, hogy első lépésben meghatározzuk a kritikus értéket mely fölé 0,05 valószínűséggel kerülhet a mintaátlag értéke.

Ezt az értéket láthatjuk a sűrűségfüggvényen ábrázolva és Excelben számítva.

Ha a mintaátlag értéke ennél nagyobb azt mondjuk, hogy nem tulajdonítható a 12-től való fölfelé eltérés ekkora mértéke kizárólag a véletlennek.

Annak  valószínűsége hogy a  mintaátlag ennyire eltér a feltételezett várható értéktől  nagyon kicsi – a megengedett elsőfajú hibavalószínűséggel egyenlő – ezért ekkor azt feltételezzük hogy az eltérés mértéke döntően abból a hatásból ered, hogy 12-nél nagyobb a tanuló átlagos futóteljesítménye 100 m-en, így  nem igaz a tanuló állítása, a nullhipotézist el kell vetnünk és az alternatív hipotézist kell igaznak vennünk.

Az alternatív hipotézist a statisztikai irodalmakban gyakran ellenhipotézisként is nevezik.

Ekkor a kritikus tartomány azon valós számok halmaza melyek értéke legalább  .

Elfogadási tartomány a -nál kisebb valósak halmaza.

Ekkor ha a minta átlaga az elfogadási tartományba esik azt mondjuk a tanuló állítása igaz, a nullhipotézist elfogadjuk 0,05 elsőfajú hibavalószínűség mellett.

Az alternatív hipotézist ekkor elvetjük.

A mért eredményeken a mintaátlag .

A kritikus érték a mintaátlag eloszlása alapján: .

Mivel  így a mintaátlag az elfogadási tartományba esik ekkor a nullhipotézist elfogadjuk.

Az elfogadási tartomány meghatározására Excelben használhatjuk a NORM.INVERZ függvényt, mely meghatározza azt az értéket mely az elfogadási tartomány felső határa, az elutasítási tartomány legkisebb értéke.

A kritikus értéket hasonló gondolatmenettel vezethetjük le mint a konfidencia intervallum végpontjának meghatározását csak ebben  feladatban nem egy origóra szimmetrikus intervallumban keressük a minta értékét a standard normális eloszlássegítségével hanem egy olyan  kritikus értéket keresünk melyre:

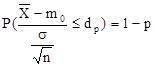
ahol a megengedett elsőfajú hibavalószínűség.

A standard normális eloszlás eloszlásfüggvényével kifejezve:

Ekkor az elfogadási tartomány:

Ekkor a kritikus érték:

Kritikus érték direkt számítása Excel függvénnyel:

Ennek kapcsán tárgyalnunk kell az alternatív hipotézisek fajtáit.

A nullhipotézis alakja, mint ahogy elnevezéséből következik az eloszlás egy paraméterétől való 0 eltérés feltételezése.

Az előbbi feladatban a nullhipotézis alakja a következő volt:

A feladat jellegéből következett, hogy alternatív hipotézisként

állítást fogalmaztunk meg. Ha ugyanis a tanulóról a mérés kapcsán kiderül, hogy jobb átlagidőt fut mint a teljesítési szint azaz 12 sec/100m akkor is igazat állít.

Ezt az alternatív hipotézist jobboldali alternatív hipotézisnek nevezzük mivel a kritikus tartomány egy adott értékhez képest vele egyenlő vagy nála nagyobb értékek halmaza:

Lehetnek azonban olyan tipusú feladatok például egy termék súlya vagy  hossza egy gyártási feladat kapcsán vagy egy szállítás ideje egy szállítási feladatban amikor az sem jó ha a nullhipotézisben megfogalmazott értéknél kisebb az sem jó ha nagyobb értéket kapunk a mérés során.

Ekkor az alternatív vagy ellen hipotézis alakja a következő:

Ezt kétoldali alternatív vagy ellen hipotézisnek nevezzük.

Nézzük meg ezt egy példán keresztül:

Egy versenyen a 100 m es síkfutás szintidejét 12 sec-ban állapították meg.

A szintidőre időnként méréseket végeznek hogy korrigálni kell-e?

50  versenyzőnek felmérték az idejét és az alábbi időket kapták.

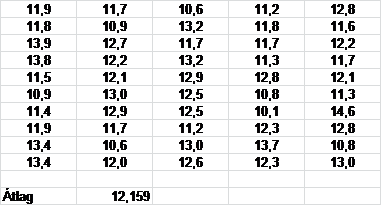
Tudjuk hogy az eredmények normális eloszlást mutatnak melynek szórása 1sec.

Továbbra is a megengedett elsőfajú hibavalószínűség.

Kérdés, hogy  meg kell-e változtatni a szintidőt a megállapítotthoz képest?

Ebben az esetben két kritikus értékünk van az -ra szimmetrikusan.

A felső kritikus érték számítása:

Felső kritikus érték számítása Excel függvény alapján:

Az alsó kritikus érték számítása:

Az alsó kritikus érték számítása Excel függvény alapján:

Itt az elfogadási tartomány a (11,723;12,277) intervallum.

Mivel a mintaátlag 12,159 így azt a következtetést vonhatjuk le, hogy tulajdonítható a 12-től való felfelé eltérés ekkora mértéke kizárólag a véletlennek, ezért a nullhipotézist elfogadjuk.

Ebből azt a következtetést kell levonni a döntéshozónak,  hogy  a szintidőt nem kell csökkenteni.

Kétoldali alternatív hipotézis ábrázolása :

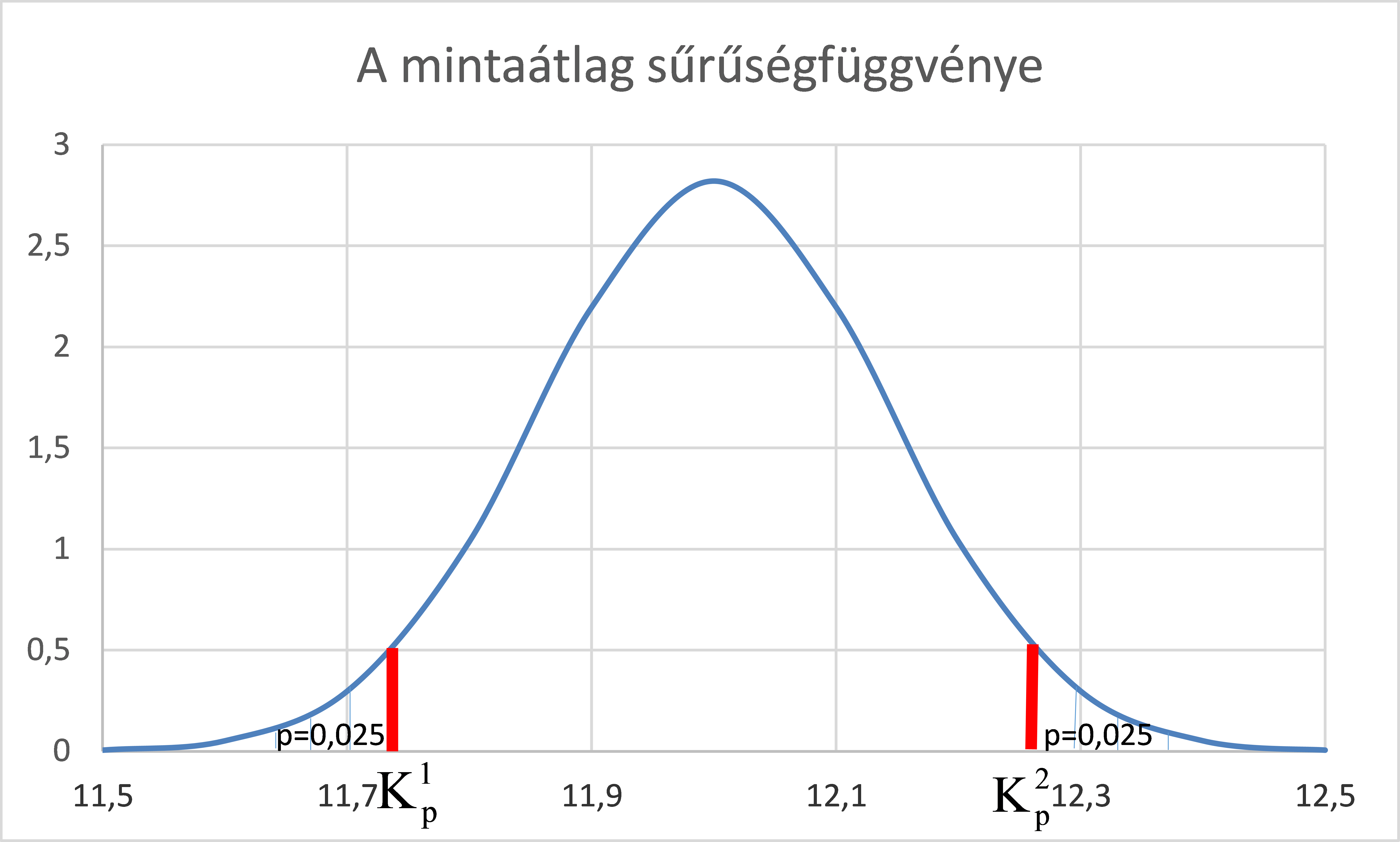
Kétoldali alternatív hipotézis, kritikus értékek számítása.

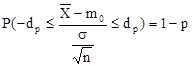
Kihasználva a standard normális eloszlás eloszlásfüggvényére megismert összefüggést:

Kapjuk, hogy:

     Ez azt jelenti hogy egy

• olyan  felső kritikus értéket számolunk mely fölé 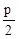 valószínűséggel esik a mintaátlag,

és hasonlóan

• olyan alsó kritikus értéket számolunk mely alá 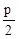 valószínűséggel esik a mintaátlag

Így a kritikus értékek:

Baloldali alternatív hipotézis:

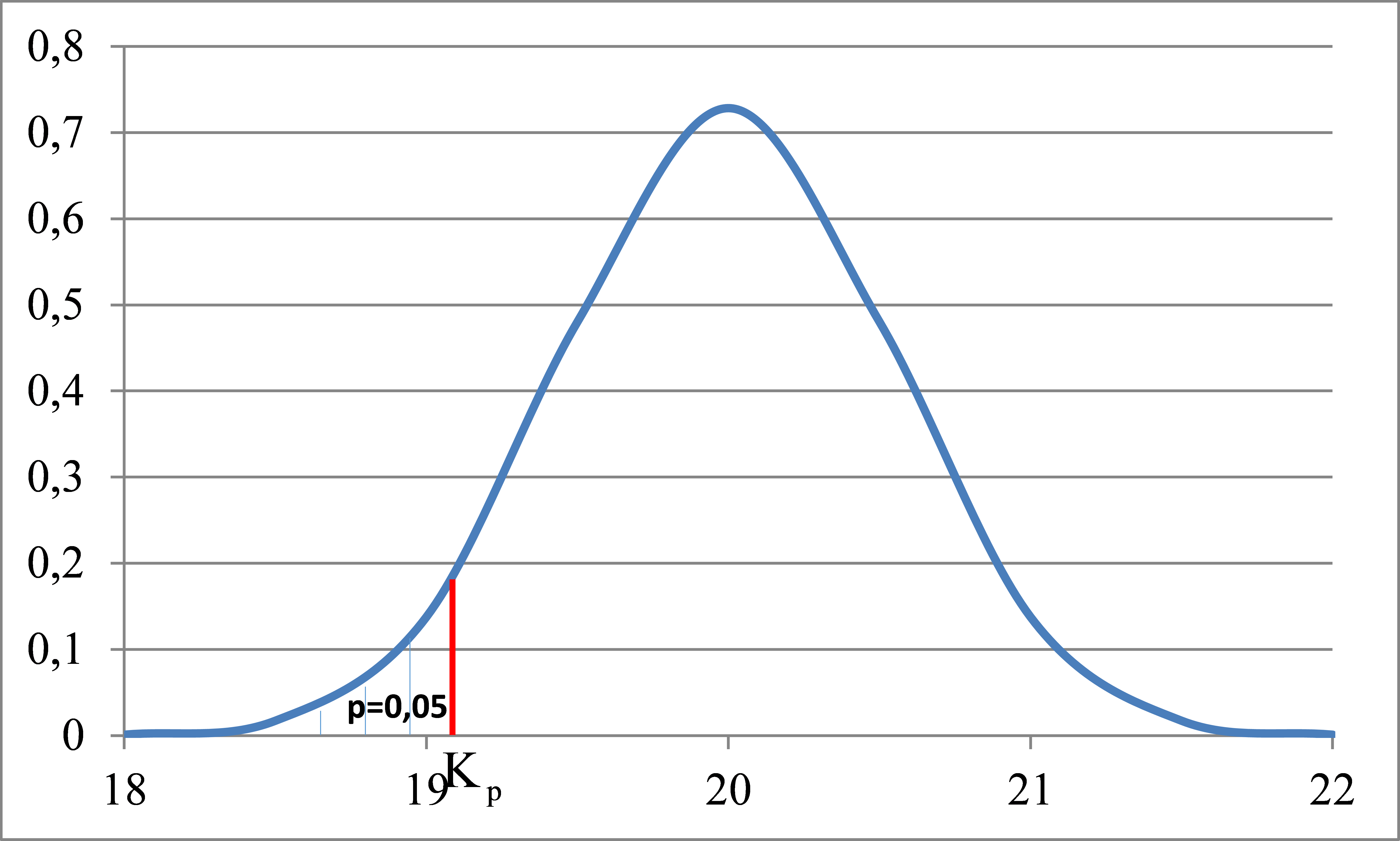
Egy diszkoszvető versenyen indulni szándékozó tanuló versenyző azt állítja dobóteljesítményével teljesíti  a 20 m-es nevezési szintet.

30 dobást végzett, melyek az alábbiak:

A dobások szórása ismert, .

megengedett elsőfajú hibavalószínűség mellett elfogadható-e az állítás?

Ekkor  .

A nullhipotézis a következő:         

Nyilván ha jobb a teljesítménye mint a nevezési szint, akkor állítása igaz.

Ezért a következőt fogalmazhatjuk meg.

Alternatív vagy ellen hipotézis: 

Kritikus érték számítása Excel függvénnyel

Baloldali alternatív hipotézis ábrázolása: