Szórás

Önmagában a várható érték nem ad elegendő jellemzést az valószínűségi változóról, mert nem mondja meg hogy az értékei mennyire vannak közel az átlaghoz, azaz az átlag valós jellemzője-e a változó értékeinek ?

Ennek mértékét jellemezzük az átlagtól való átlagos eltéréssel, a szórással.

Ez a két jellemző együtt már pontosabb képet az változó viselkedéséről.

Legyen  egy valószínűségi változó akkor az  is egy valószínűségi változó így

is az.

Ennek várható értékét nevezzük a változó szórásnégyzetének.

Ebből a szórás:

Igaz az alábbi állítás:

Legyenek  konstansok és  páronként független valószínűségi változók akkor:

Az  egyenlőség könnyen igazolható és módot ad a szórás egyszerűbb kiszámítására.

A kockadobás változójának szórásnégyzete  így kétféleképp számítható:

• definíció alapján:

vagy

• a definícióból származtatott 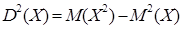 formula segítségével:

Így a kockadobás változójának szórása: .

Ha véges sok értéket vesz fel a változó akkor a szórását a statisztikai SZÓRÁS függvények egyikével számoljuk aszerint, hogy statisztikai minta alapján adunk a sokaságbeli szórásra becslést vagy amit kezelünk az teljes  sokaság és ennek szórását számoljuk. Ezen belül az ÁTLAG függvénynek megfelelően itt is abban tér el a kétféle SZÓRÁS függvény, hogy a logikai és szöveges értékeket kezeli-e?

Kockadobás esetében például a SZÓRÁSPA függvény a fentebb számítottakkal azonos eredményt ad.

Excelben a SZÓR.M, SZÓR.S, SZÓRÁSA, SZÓRÁSPA  függvényekkel tudunk szórást számítani.

• a SZÓR.M és a SZÓRÁSA függvények mintának tekintik az adatokat és a későbbi statisztikai fejezetben a minta szórásának tekintett formula alapján számít szórás értéket

• Sokaságnak tekintik az adatokat és így számolnak szórást a SZÓR.S és a  SZÓRÁSPA függvények, a SZÓRÁSPA szöveg és logikai változókat is kezel.