Műveleti tulajdonságok
Hasonlóan a halmazelméleti, vagy a valós számok közötti műveletekhez itt is fontos vizsgálnunk hogy az események közötti műveletek milyen tulajdonságokkal rendelkeznek.
Az események közötti műveletekre teljesülnek a következők:
Az összeadás és szorzás művelete kommutatív (a komponensek felcserélhetők),
asszociatív (a komponesnek csoportosíthatók) és a szorzás az összeadásra nézve
valamint az összedás a szorzásra nézve disztributív, azaz a szorzás összegen komponensenként végezhető és az összeadás szorzaton komponensenként végezhető, azaz:
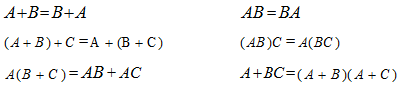
A disztributivitásból következik a beolvasztási szabály:
Eseményalgebrában is teljesülnek a logikából és a halmazelméletből jól ismert De-Morgan azonosságok:
A halmazelmélethez hasonlóan értelmezzük az alábbi műveleteket:
Definíció: Kivonás 
.
Definíció: Szimmetrikus differencia 
.
A szimmetrikus differenciára igazak az alábbi összefüggések:
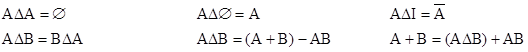
Reláció események között:
Definíció: Ha az 
esemény bekövetkezése esetén mindig bekövetkezik a 
esemény is akkor azt mondjuk, hogy az esemény maga után vonja eseményt.
Jelölés: A
B
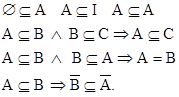
Definíció: 
eseményekről azt mondjuk, hogy teljes eseményrendszert alkotnak, ha
- egyik sem a lehetetlen esemény,
- páronként kizáróak és
- összegük a teljes esemény, azaz:
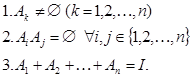
Definíció: Egy eseményt összetett eseménynek nevezünk, ha előállítható két -tól különböző esemény összegeként, azaz: 
ahol 
.
Ha egy eseményalgebra elemeinek száma n akkor az összes események száma – egy halmaz összes részhalmazainak számával analóg módon- :
