Normális eloszlás

Definíció: Egy valószínűségi változó normális eloszlású ha sűrűségfüggvénye a teljes valós számhalmazon értelmezett alábbi függvény:

ahol  tetszőleges valós,  pedig pozitív valós.

Ekkor a változó eloszlásfüggvénye a sűrűségfüggvény integrálfüggvénye.

Erre a változóra  és .

Azt hogy X valószínűségi változó várható értékű és  szórású normális eloszlású változó a következőképpen jelöljük:

Igaz a következő:

Definíció:Ha  akkor a következőképpen definiált  is valószínűségi változó és    vagyis olyan normális eloszlású valószínűségi változó melynek várható értéke 0, szórása pedig 1.

Az ilyen változót  standard normális eloszlású változónak hívjuk.

Sűrűségfüggvényére és eloszlásfüggvényére speciális jelölést alkalmazunk sűrűségfüggvényét  eloszlásfüggvényét pedig  jelölje.

A standardizálással a következő függvénytranszformációkat hajtjuk végre:

a sűrűségfüggvény esetén:

az eloszlásfüggvényre pedig:

A standard normális eloszlású változó sűrűségfüggvénye :

eloszlásfüggvénye pedig:

A normális eloszlás sűrűség és eloszlásfüggvényét Excelben tudjuk ábrázolni:

Erre szolgál a NORM.ELOSZL függvény.

NORM.ELOSZL(x;Középérték;Szórás;Eloszlásfüggvény)

X                     : Az az érték, amelynél az eloszlást kiszámítjuk

Középérték     : Az eloszlás várható értéke

Szórás             :  Az eloszlás szórása.

Eloszlásfv       :  Ha IGAZ az eloszlásfüggvényt ad vissza ha HAMIS, akkor sűrűségfüggvényt

Az alábbiakban egy N(0,1) és egy N(7,4) változó sűrűségfüggvényért láthatjuk.

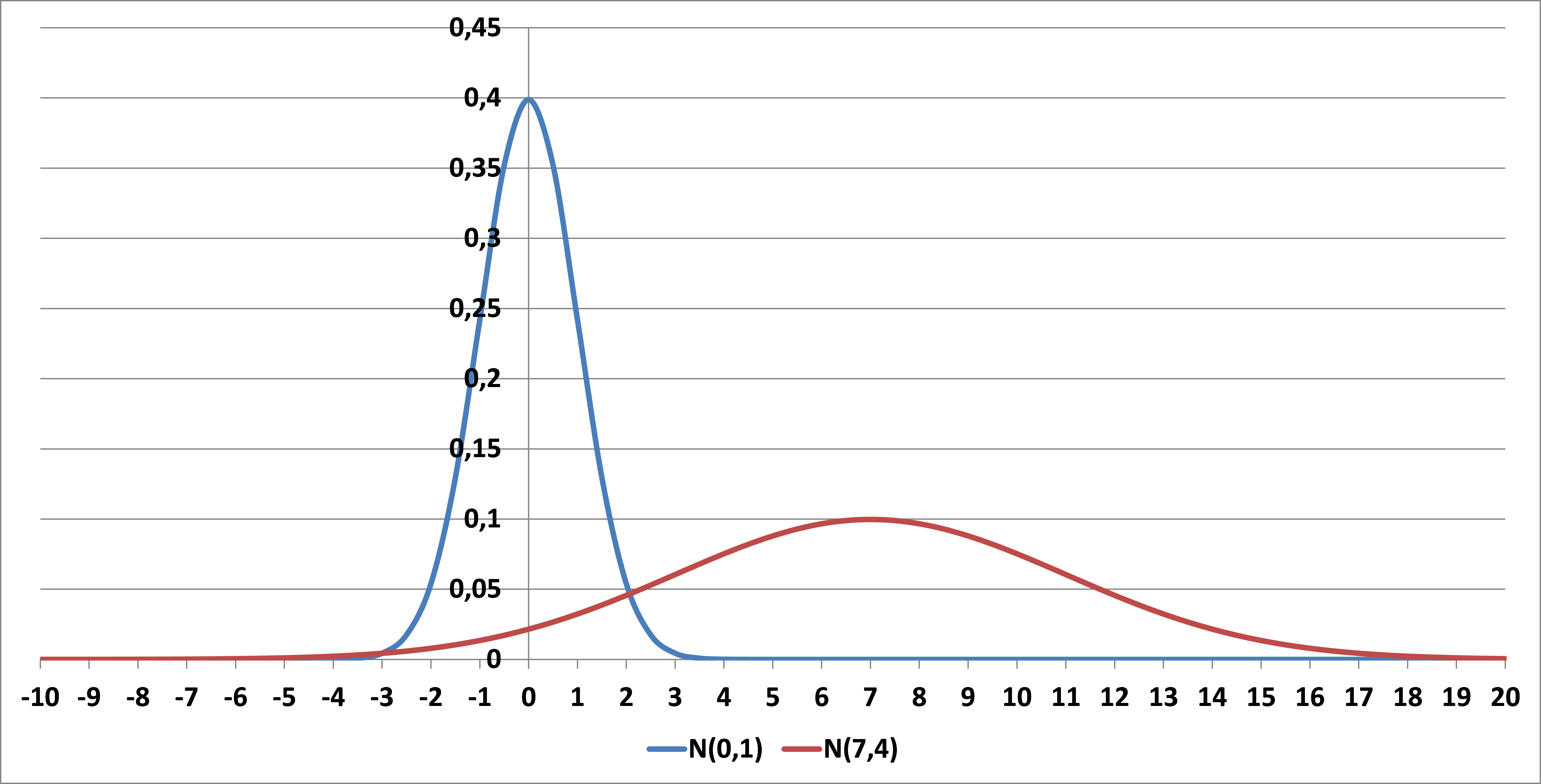
A normális eloszlás sűrűség függvényét haranggörbének(vagy Gauss-féle haranggörbének) hívjuk.

A függvény lefutásában nagyon forntos szerepe van a paramétereknek.

A függvény szimmetrikus és maximuma helyen van.

Az  illetve  x koordinátájú pontokban pedig inflexiós pontja van.

Így a standard normális eloszlás sűrűségfüggvényének -1 és +1 pontokban az N(7,4) sűrűségfüggvényének pedig 3 és 10 pontokban.

Így azt láthatjuk hogy a szórás növelésével a görbe kisebb kisebb maximumú  lesz és  a függvény alatti terület azonos %-át, pl:95%-át  nagyobb intervallumon veszi fel.

Ugyanezen változók eloszlásfüggvényei az alábbiak:

Látható hogy a szórás növelésével az eloszlásfüggvény kevésbé lesz meredek.

Fontos megjegyezni, hogy a sűrűségfüggvény tengelyesen szimmetrikus az egyenesre, az eloszlásfüggvény pedig középpontosan szimmetrikus az  pontra .

A standard normális eloszlás szimmetriáját a következő formula írja le:

 .