Várható érték becslése ismeretlen szórás esetén
Tegyük fel, hogy 
ahol az eloszlás egyik paramétere sem ismert.
Konfidencia intervallumot szeretnénk szerkeszteni a várható értékre.
Az előző részben tárgyalthoz hasonló lesz a statisztika, csak az ismeretlen szórást helyettesítjük a minta szórásával.
Így statisztikánk az alábbi formát ölti:
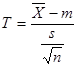
Ez a statisztika 
szabadságfokú Student féle t-eloszlású valószínűségi változó lesz.
Így szokták jelölni 
-vel vagy 
-gyel is.
Jelöljük az n-1 szabadságfokú Student féle t-eloszlású valószínűségi változó eloszlásfüggvényét 
-vel.
Mivel a Student eloszlás sűrűségfüggvénye a standard normális eloszlás sűrűségfüggvényéhez hasonlóan az y tengelyre szimmetrikus, ezért eloszlásfüggvényére ugyanaz a szimmetriatulajdonság igaz mint a standard normális eloszlás eloszlásfüggvényére.
Azaz igaz, hogy tetszőleges 
szabadságfok esetén
Így a konfidencia intervallum kiszámításakor kapjuk, hogy, kiindulva az alábbi egyenletből:
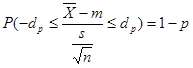
A konfidencia intervallumot meghatározó egyenlőtlenség a következő alakban írható fel:
Legyen egy normális eloszlású sokaságból vett minta mint a mellékelt táblázatban.
A szórás nem ismert. A várható értékre szeretnénk konfidenciaintervallumot adni.
Számítsuk ki meg a konfidenciaintervallum végpontjait 
valószínűség mellett.
Ennek meghatározása Excelben ugyanúgy történhet mint normális eloszlás esetén, a konfidencia intervallum fent felírt formulája alapján:
T.INVERZ statisztikai függvénnyel
a MEGBÍZHATÓSÁG.T függvény alapján:
