8.1. Szöveges feladatok
A szöveges feladatok általában olyan problémák, amelyek valamilyen szituációt írnak le.
A szöveges feladatok szerepe a tanításban:
- műveletek értelmezése, elmélyítése
- szövegértési képesség fejlesztése
- problémamegoldó gondolkodás fejlesztése
A szöveges feladatokat 6. osztályban még következtetéssel oldjuk meg. A cél ekkor a problémamegoldás lépéseinek gyakorlása. Az adatok kigyűjtése, a szövegértés, az összefüggések ábrázolása, akkor is szükséges és hasznos, ha később egyenletet írunk fel a feladat megoldásához.
A szöveges feladatok megoldásának lépései megfelelnek a problémamegoldás lépéseinek:
- A szöveg elolvasása (hangosan is), esetleg eljátszása.
- Mi a kérdés?
- Keressük meg a kérdés megválaszolásához szükséges adatokat!
- Keressünk összefüggéseket, rajzoljunk ábrát, írjunk fel műveleteket, azaz keressük meg a szöveg matematikai modelljét.
- Végezzük el a műveleteket!
- Ellenőrzés. A matematikai eredményt visszafordítjuk az eredeti szituációra.
- Válasz a kérdés újra olvasása után.
Írjunk minél többet!
A szöveges feladatok megoldásának a szövegértés az egyik legfontosabb eleme. Ezt segíthetjük azzal, ha a feladat szövegét fokozatosan egyre vázlatosabban írjuk le, így az összefüggések is világosabbak lesznek a gyerekek számára. A megoldások során is érdemes a gondolatokat írásban lejegyezni, ez tudatosítja a megoldási módot, világosabbá teszi a lépéseket, így más hasonló feladatok megoldásánál is alkalmazható tudást hoz létre.
A szöveges feladatok csoportosítása
- A kérdés helye lehet
- a feladat elején – egységessé tesz feladatsort, ha lehetőség szerint kérdőszóval kezdődnek a feladatok
- a feladat közepén – a legnehezebben érzékelhető a gyerekek számára.
- a feladat végén – az olvasás utolsó eleme, jó kiindulás a megoldáshoz.
- Az adatok száma szerint
- hiányos feladat – meg kell szereznünk a hiányzó adatot
- pontosan annyi adat van, amennyi szükséges
- felesleges adatok vannak – ki kell választani a szükségeseket
- A feladat szövegezése
- egyenes
- fordított – ilyen feladatokkal találkoztunk az összeadásra vezető szöveges feladatoknál.
- A feladat bonyolultsága
- egylépéses – egy művelettel megoldható
- kétlépéses – két lépésben megoldható, nehézséget jelent a gyerekeknek a részfeladatok meghatározása
- többlépéses – több lépés megtervezése szükséges.
- A megoldási módok
- próbálgatás – csak akkor számít teljes megoldásnak, ha az összes esetet végignéztük. A próbálgatás segít megismerni a problémát, megtalálni a szabályosságokat, amelyeket aztán igazolni kell. Semmiképp se alkalmazzuk folytonosan változó mennyiségeknél, például eltelt időre vonatkozó feladatokat nem lehet percenkénti próbálgatással megoldani.
- visszafelé következtetés (rákmódszer, buborék módszer)
- összefüggések ábrázolása szakaszokkal
Példa: Egy horgásztól megkérdezték, hogy hány halat fogott. Ő így felelt: „Azt reméltem, hogy húszat fogok, de ha háromszor annyit fogtam volna, mint amennyit fogtam, akkor is 2-vel kevesebbet fogtam volna, mint amennyit reméltem.” Hány halat fogott?
1. Megoldás: Gondolkodjunk visszafelé!
A fogott halak száma kerül az első buborékba, a háromszorosa a következőbe, még ezt sem tudjuk egyelőre. Ennél 2-vel nagyobb szám a remélt halak száma a 20.
A műveleteket a buborékok közötti nyilakkal jelöljük:
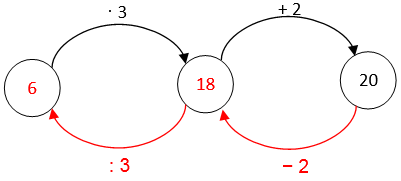
Ellenőrzés: 6 · 3 + 2 = 20.
Válasz: Tehát a horgász 6 halat fogott.
2. Megoldás: Ábrázoljuk szakaszokkal a halak számát!
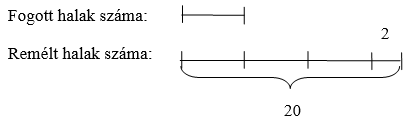
A rajzról leolvasható, hogy a fogott halak száma (20 – 2) : 3 = 6.
A példa kétféle megoldása azért is fontos, hogy a gyerekek lássák, hogy a feladatokat nemcsak egyféle módszerrel lehet megoldani.
- A megoldások száma
- egy megoldás
- több megoldás – az összes megoldást meg kell adni
- nincs megoldás – a feladat megoldása az, hogy nincs megoldás.
Példa: Keressük meg az összes olyan páratlan, öttel osztható háromjegyű számot, amelyben a számjegyek összege 4!
Megoldás: Az öttel osztható számok 0-ra vagy 5-re végződnek. Mivel a szám páratlan, ezért 5-re végződik, így számjegyeinek összege legalább 5, ami nagyobb a 4-nél, tehát nincsen a feladat feltételeinek megfelelő szám.