2.2. Számegyenes

A számegyenes a számok univerzális modellje, a számok geometriai szemléltetésének eszköze.

Számegyenest kapunk, ha egy egyenesen kijelöljük:

-a növekedés irányát,

-egy viszonyítási pontot,

-egy egységet.

Ezután az egység többszöröseit felmérve tetszőleges természetes számot ábrázolhatunk. Így a számoknak az egyenes pontjai felelnek meg. Természetes számok esetén a számnak megfelelő pont az egyenesen annyi egység távolságra van a 0-nak megfelelő ponttól, amennyi a szám.

A számegyenesen rendszerint a 0 és az 1 számok helyének kijelölésével adjuk meg a viszonyítási pontot és az egységet, de ez nem szükségszerű.

Példa: Keressük meg a 0 helyét a számegyenesen!

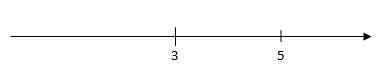
Megoldás: A 3 és az 5 számok helye két egység távolságra van egymástól, így az általuk meghatározott szakasz hosszának fele az egység. Ezután a 0 helye már könnyen meghatározható: 3 egységet lépünk balra a 3-as szám helyétől.

 

A számegyenes egységének és viszonyítási pontjának megválasztása az ábrázolandó számoktól függ.

Például  a 340; 341; 342 számok ábrázolásához célszerű a számegyenesnek a 328 és 345 közötti részét lerajzolni úgy, hogy egy szakasz  egy egységnek felel meg.

Azonban a 340; 350; 360 számok ábrázolása esetén egy szakasz 10 egységnek feleljen meg.

A számegyenes segít az összeadás, kivonás szemléltetésében, amelyeket padlóra rajzolt számegyenesen való lépkedéssel is lejátszhatunk.

A számegyenes megkönnyíti a negatív egész számok bevezetését, mint a hőmérő modell univerzális megfelelője.

A számegyenesen a természetes számokat pontokként jelöljük. 5. osztálytól szükség van feltételeknek megfelelő számhalmazok ábrázolására, amelyeket már szakaszokkal jelölünk, és a szakaszra eső természetes számokat, a számkör bővítésével a szakaszra eső racionális számokat tekintjük megoldásnak. A szakaszok végpontjait teli karikával jelöljük, ha a végpont hozzátartozik a számhalmazhoz, és üres karikával, ha nem tartozik hozzá.

Például az alábbi számegyenesen a 3-nál nagyobb, és 5-nél nem nagyobb számokat ábrázoltuk. A természetes számok körében a 4 és az 5 felel meg a feltételeknek.

A törtek számegyenesen való ábrázolásához az egységet egyenlő részekre osztjuk. A tananyagok tanításának sorrendje szempontjából lényeges, hogy különböző nevezőjű törteket akkor tudnak a gyerekek egy számegyenesen ábrázolni, ha már tudnak törtet egyszerűsíteni, bővíteni, hiszen az egységet annyi egyenlő részre kell osztani, amennyi a két tört közös nevezője. Ugyanez szükséges a törtek összehasonlításához is.

A számegyenes lehetőséget ad a valós számok szemléltetésére a gyerekek számára: a számegyenes pontjainak megfelelő számokat tekintjük valós számoknak.