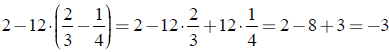3.3. Műveleti azonosságok
További műveleti tulajdonságokat sorolunk fel bizonyítás nélkül, amelyeket számokkal a gyerekeknek is megmutatunk, ezen kívül a számkörbővítéskor hasznos lesz a törtekkel és az egész számokkal végzendő műveletek definiálásához.
Fontos, hogy a gyerekek ne gondolják, hogy ha egy összefüggés néhány számra igaz, akkor minden számra is igaz lesz. Ezért az azonosságokat szemléltetjük számukra, valamint az egyenlőség két oldalán álló kifejezések egy szöveges feladat megoldásának kétféle kiszámítási módját adják, mivel mindkettő helyes, ezért a két kifejezés egyenlő. Ez úgynevezett „prebizonyítás”, amely már tartalmazza a bizonyítás gondolatmenetét, a következtetést, de még konkrét példán keresztül mutatja be ezeket.
A disztributivitásra vonatkozó „prebizonyítás” a következő:
Példa:
Kati 2 gombóc, Peti 3 gombóc fagylaltot vásárolt. Mennyit fizettek összesen, ha egy gombóc ára
Megoldás:
Számolhatunk úgy, hogy ketten külön-külön fizetnek, ekkor Kati 2 · 160 Ft-ot, Peti 3 · 160 Ft-ot fizetett, ketten együtt 2 · 160 + 3 · 160 Ft-ot fizettek.
Ha ketten együtt fizetnek, akkor összesen 2 + 3 gombóc fagylaltot vesznek, így (2 + 3) · 160 Ft-ot fizetnek.
A kétféle számítási mód ugyanazt az eredményt adja, ezért:
2 · 160 + 3 · 160 = (2 + 3) · 160.
A természetes számok körében 5. osztályban foglalkozunk az összeg, különbség, szorzat, hányados változásaival. Vigyázzunk arra, hogy ezeket az összefüggéseket a gyerekeknek ne kelljen szabályként megtanulni! Változatos feladatokkal érjük el, hogy tudják alkalmazni az összefüggéseket! Ezek közül most a különbséget és a hányadost emeljük ki.
Minden m > n és k természetes számra:
m – n = (m + k) – (n + k),
m – n = (m − k) – (n − k),
azaz a különbség nem változik, ha a kisebbítendőhöz és a kivonandóhoz ugyanazt a természetes számot hozzáadjuk vagy kivonjuk. Ez azt jelenti, hogy a természetes számok többféleképpen írhatók fel különbség alakban.
Minden m, n≠0 és k≠0 természetes számra, ahol m az n többszöröse, és mindkettő többszöröse k-nak:
m : n = (m · k) : (n · k),
m : n = (m : k) : (n : k),
azaz a hányados nem változik, ha az osztandót és az osztót ugyanazzal a 0-tól különböző természetes számmal szorozzuk vagy osztjuk. Ez azt jelenti, hogy a természetes számok többféleképpen írhatók fel hányados alakban. Ez az összefüggés az alapja az egyenes arányosságnak.
Minden m, n és k≠0 természetes számra
m · n = (m · k) · (n : k)
m · n = (m : k) · (n · k)
azaz a szorzat nem változik, ha az egyik tényezőt ugyanazzal a 0-tól különböző természetes számmal szorozzuk, mint amivel a másik tényezőt osztjuk. Ez az összefüggés az alapja fordított arányosságnak.
Összegből úgy vonunk ki egy számot, hogy az összeg egyik tagjából vonjuk ki a számot, és a különbséghez hozzáadjuk az összeg másik tagját:
(m + n) – k = (m – k) + n és (m + n) – k = m + (n – k).
Szorzatot úgy osztunk el egy számmal, hogy a szorzat egyik tényezőjét osztjuk el a számmal, és a hányadost szorozzuk a szorzat másik tényezőjével:
(m · n) : k = (m : k) · n és (m · n) : k = m · (n : k).
Ezeket az azonosságokat a gyerekek hajlamosak összekeverni a disztributivitással, és az összeg mindkét tagjából kivonják a számot, vagy a szorzat mindkét tényezőjét osztják a számmal. Hasonló összefüggések érvényesek, amikor összeghez hozzáadunk egy számot, és amikor szorzatot szorzunk egy számmal.
Összeg, különbség kivonása:
Minden m > n + k természetes számokra:
m – (n + k) = (m – n) – k
m – (n – k) = (m – n) + k
Szorzattal, és hányadossal való osztás:
m : (n · k) = (m : n) : k
m : (n : k) = (m : n) · k
Lényeges, hogy ezeket az azonosságokat mindkét irányba tudják alkalmazni a gyerekek. Az azonosságokat természetes számokkal kezdik bevezetni, majd az algebrai kifejezéseknél újra előkerülnek, hiszen amit a gyerekek számokkal tudnak, nem biztos, hogy betűkkel végzett műveleteknél is tudják.
Különbségek összege is különbség:
Minden m>n és k>l természetes számokra
(m – n) + (k – l) = (m + k) – (n + l)
Különbségek szorzata is különbség:
Minden m>n és k>l természetes számokra
(m – n)(k – l) = (mk + nl) – (ml + nk)
Hányadosok összege is hányados:
Minden m, n és k,l ≠0 természetes számra
(m : k) + (n : k) = (m + n) : k, ha az osztó azonos, és
(m : k) + (n : l) = (ml + nk) : kl, ha az osztó nem azonos.
Hányadosok szorzata is hányados:
Minden m, n és k,l ≠0 természetes számra
(m : k)(n : l) = (mn) : (kl)
Az azonosságokat célszerű úgy gyakoroltatni a gyerekekkel, hogy a műveletsor számolása praktikusabb az azonosság alkalmazásával.
Példa:
Végezzük el a következő műveletet!
(462 + 258) – ( 258 + 62)
Megoldás:
A zárójel felbontásával:
(462 + 258) – ( 258 + 62) = (462 – 62) + (258 – 258) = 400 + 0 = 400.
Különösen a törtekkel való számolásnál jelenthet könnyebbséget az azonosságok alkalmazása:
Példa:
Végezzük el a következő műveletet!
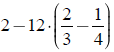
Megoldás:
Ha 12-vel beszorzunk, akkor egyszerűsíthetjük a törteket, nem kell közös nevezőre hozni.