13.8. Gráfok

Az összeszámlálási feladatoknál gyakran alkalmazzuk a gráfokkal való ábrázolást. A gráfokkal kapcsolatban önmagukban is érdekes problémákkal találkozhatunk.

A gráf pontokból és élekből áll. A gráf élei lehetnek irányítottak, akkor irányított gráfról beszélünk.

Példa: Péntek este öt barátnő közül többen beszéltek egymással telefonon (bármely két lány legfeljebb egyszer beszélt egymással). Másnap megbeszélték, hogy ki hány barátnőjével beszélt (ötük közül). Hány beszélgetés zajlott az öt lány között péntek este, ha egyszerre mindig ketten beszéltek egymással, és

a) Kati 4, Jutka 1, Nóri 3, Marcsi és Bori 2-2 barátnőjével beszélt;

b) Kati 3, Jutka 1, Nóri 1, Marcsi és Bori 2-2 barátnőjével beszélt?

Megoldás:

a) Ábrázoljuk gráffal a beszélgetéseket, a pontok a lányokat jelentik, két pont össze van kötve éllel, ha a pontoknak megfelelő lányok telefonáltak egymásnak.

Kati mindenkivel beszélt, Jutka csak 1 lánnyal, aki biztos, hogy Kati. Nóri Katin kívül még 2 lánnyal beszélt, ezek csak Marcsi és Bori lehettek, mert Jutka nem beszélt velük. Ezzel Marcsinak és Borinak is megvan a 2-2 beszélgetése. Összesen 6 beszélgetést folytattak az ábra szerint.

2. megoldás: Ha összeadjuk az egy-egy lány által folytatott beszélgetések számát, akkor 4+3+2+2+1=12-t kapunk. Ez épp a kétszerese a beszélgetések számának, mert minden beszélgetést mind a két résztvevőnél számoltuk. Tehát a beszélgetések száma: 12/2=6.

b) A beszélgetések gráfját hiába próbáljuk lerajzolni, nem sikerül. Be kell bizonyítani, hogy ez az eset valóban nem lehetséges.

Ebben az esetben az egy-egy lány által folytatott beszélgetések számának összege 3+1+1+2+2=9. Minden beszélgetésben ketten vesznek részt, így a beszélgetések száma 9/2, ami nem egész szám, ezért ez az eset nem lehetséges, valaki rosszul emlékezett beszélgetései számára.

Gráf pontjainak fokszámának  nevezzük a pontból induló élek számát.

Minden gráfban a pontok fokszámának összege páros, az élek számának a kétszerese.

A gráfban a fokszámok összege az élvégek számának összege. Mivel minden élnek két vége van, a fokszámok összege az élek számának kétszerese, következésképpen a fokszámok összege páros.

A fenti tétel másik megfogalmazása:

Minden gráfban a páratlan fokszámú pontok száma páros.

 

Példa: Hány mérkőzést játszott öt csapat a körmérkőzéses bajnokságban (minden csapat játszott mindegyik másikkal egyszer)?

Megoldás:

Ábrázoljuk gráffal a bajnokságot: a csapatok a pontok, az őket összekötő élek a meccseket jelentik.

Az ábráról leolvasható, hogy 10 meccset játszottak.

2. megoldás: Mind az 5 csapat 4 másikkal játszott. Ez 5∙4 meccs lenne, de ekkor minden meccset mindkét résztvevőnél számoltuk, ezért osztani kell 2-vel. A mérkőzések száma:  .

Ha egy gráf pontjai között az összes lehetséges élt behúzzuk, akkor teljes gráfot kapunk. Az n pontú teljes gráf éleinek száma .

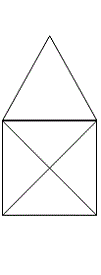
Példa: Rajzoljuk meg az alábbi ábrákat a ceruza felemelése nélkül úgy, hogy minden vonalon pontosan egyszer haladunk át! (A vonalak metszéspontján többször is átmehetünk.)

a)

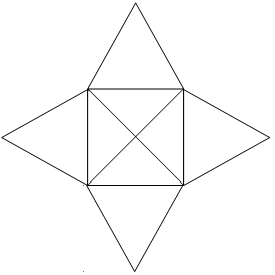
b)

Megoldás:

Némi próbálkozás után az első ábrát meg tudják rajzolni a gyerekek, a másodikat azonban nem. Az a) eset megoldásánál minél több rajzot nézzünk meg, és vegyük észre, hogy mindegyik vonal két végpontja a házikó bal alsó és jobb alsó sarka. Több hasonló ábra rajzolása után észre lehet venni, hogy két eset lehet:

- a vonal zárt, azaz a kezdőpontja és a végpontja azonos, ekkor az ábra pontjai mind olyanok, hogy páros számú szakasz indul belőlük, azaz a pontok fokszáma páros;

- a vonal nem zárt, ekkor a kezdőpont és a végpont fokszáma páratlan, a többi pont fokszáma páros.

Ha a feltételnek megfelelő vonal áthalad egy ponton, akkor egy élen bemegy, egy élen kijön, kettőt használ el a pontba futó élekből, ezért minden nem végpont fokszáma páros kell legyen. Ha a vonal két végpontja megegyezik, akkor ennek a pontnak a fokszáma is páros, ha pedig különbözik, akkor mindkét pont fokszáma páratlan, hiszen az egyikből csak kijön a vonal, a másikba pedig csak bemegy.

Mivel a b) ábrában a négyzet minden csúcsának fokszáma páratlan, 4 páratlan fokszámú pont van, ezért ezt nem lehet egy vonallal megrajzolni.

Egy összefüggő gráf éleit akkor és csak akkor lehet egy vonallal megrajzolni a ceruza felemelése nélkül úgy, hogy minden élen pontosan egyszer haladjunk át, ha a páratlan fokszámú pontok száma 0 vagy 2.