5.2. A törtek tanítása
5. osztályban a törtek kétféle értelmezése közül az első még az alsó tagozatos törtrész értelmezésnek felel meg, de már nagyobb számokkal a szemlélettől elszakadva is használjuk.
1. értelmezés: A tört nevezője megnevezi, hogy az 1 egészet hány egyenlő részre osztjuk.
A tört számlálója megmutatja, hogy az egyenlő részek közül hányat veszünk.

2. értelmezés: A ![]() tört a 2 egésznek a harmada:
tört a 2 egésznek a harmada:
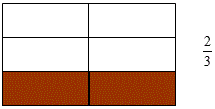
A második értelmezés közelebb visz ahhoz, hogy a törtrészből törtszám legyen:
![]() = 2 : 3.
= 2 : 3.
Ezzel a pozitív racionális számokat vezetjük be két pozitív egész szám hányadosaként, amelyeknek előbbi, törtvonallal felírt alakját közönséges tört alaknak mondjuk.
A ![]() tört kétféle értelmezésével ugyanazt kapjuk. Ezt megmutathatjuk a következő példával.
tört kétféle értelmezésével ugyanazt kapjuk. Ezt megmutathatjuk a következő példával.
Kati, Bori és Dóri kaptak két egyforma méretű tábla csokoládét, egy tej csokit és egy fehér csokit, amelyeket igazságosan elosztottak. Mindenki megkapta a két tábla csoki harmadát, egy szeletet a tej csokiból és egy szeletet a fehér csokiból. Dóri a tej csokit szerette jobban, Kati a fehér csokit, ezért cseréltek, Dórinak két szelet tej csokija lett, azaz megkapta a tej csoki tábla ![]() részét. Tehát a két tábla csoki harmada ugyanannyi, mint egy tábla
részét. Tehát a két tábla csoki harmada ugyanannyi, mint egy tábla ![]() része.
része.
Fontos, hogy a törtszámokat sokféleképpen szemléltessük, és gondoljunk arra, hogy vannak gyerekek, akiknek több tevékenységre, vizuális szemléltetésre van szükségük, mielőtt a törtekkel absztrakt módon csak számokként foglalkozunk.
Sorban tanítjuk az 1-nél nagyobb törteket, a törtek egyszerűsítését, bővítését, majd a közös nevezőre hozás alapján a törtek ábrázolását számegyenesen, és a törtek összehasonlítását. A törtfogalom mélyítése céljából nemcsak azonos nevezőjű törteket hasonlítunk össze, hanem azonos számlálójú törteket is.
Az azonos nevezőjű, majd a különböző nevezőjű törtek összeadását szemléltethetjük a törtrészekkel. A törtszámok természetes számmal való szorzását visszavezetjük összeadásra.
6. osztályban a törtek szorzását bevezethetjük egyrészt a szorzat változásai alapján, másrészt szemléletesen:
Példa:
Hány négyzetméter annak a téglalapnak a területe, amelynek oldalai ![]() m és
m és ![]() m?
m?
Megoldás:
Az ![]() m2, másrészt a nagy négyzet
m2, másrészt a nagy négyzet ![]() -ed része. Innen
-ed része. Innen  .
.
Ezt a gondolatmenetet folytatva ábrázolhatjuk azt a téglalapot, amelynek oldalai ![]() m és
m és ![]() m, és területe:
m, és területe: ![]() m2.
m2.