6.5. Prímszámok, prímtényezőkre bontás
Prímszámnak nevezzük azt a természetes számot, amelynek pontosan két osztója van.
Összetett számnak nevezzük azokat a 0-tól és 1-től különböző természetes számokat, amelyek nem prímszámok.
Matematikában megkülönböztetjük a prímszámokat és a törzsszámokat, de az egész számok halmazán ezek megegyeznek.
Törzsszámoknak nevezzük azokat a 0-tól és 1-től különböző természetes számokat, amelyeknek nincs valódi osztója.
Prímszámoknak nevezzük azokat a 0-tól és 1-től különböző természetes számokat, amelyekre igaz, hogy valahányszor osztója egy szorzatnak, osztója a szorzat valamelyik tényezőjének.
Érdekesség, hogy például a páros számok halmazán a törzsszámok és a prímszámok nem ugyanazok. Például a 6 törzsszám, mert nem bontható páros számok szorzatára. Viszont a 6 nem prímszám, mert a 6 osztója a 4 · 18 = 72-nek, mert 72 = 6 · 12, de a 6 nem osztója sem a 4-nek, sem a 18-nak (18 = 6 · 3, de a 3 nem páros, ezért a páros számok halmazán a 6 nem osztója a 18-nak).
Minden összetett szám a tényezők sorrendjétől eltekintve egyértelműen írható fel véges sok prímszám szorzataként.
Példa: Bontsuk fel a 48-at prímtényezők szorzatára!
Megoldás: Rajzoljunk ágrajzot!
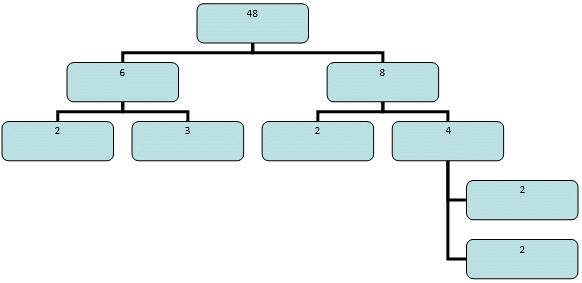
48 = 2 · 3 · 2 · 2 · 2
A prímtényezőkre bontás a pozitív egész kitevős hatvány alak megismerésével rövidebben felírható. Van, ahol már 6. osztályban bevezetik a hatvány alakot éppen a prímtényezőkre bontásnál. Hasznos az is, ha 7. osztályban a hatványozás után ismételjük a számelméletet, és a korábban tanult összefüggéseket felírjuk a hatvány alakkal.
Ez megkönnyíti az osztók számának meghatározását.
48 = 3 ·