11.3. Alakzatok
A van Hiele-féle szakaszoknak megfelelően a gyerekek felső tagozatban foglalkoznak az alakzatok definíciójával, tulajdonságaival, azok összefüggéseivel, mindenképpen a tárgyi tevékenységre, tapasztalatra alapozva.
5. osztályban a síkbeli alakzatok közül a téglalapot, négyzetet tárgyaljuk részletesen, a további sokszögek, a kör csak érintőlegesen szerepelnek. Ugyanígy térben a téglatest szerepel a tananyagban.
Fontos módszertani kérdés, hogy az általános felől haladjunk a speciális felé, vagy fordítva. Például a téglalap meghatározásával kezdjünk, és ennek speciális eseteként mutassuk meg a négyzetet, vagy a négyzetből indulva engedjünk el megszorító feltételeket, hogy olyan téglalapot kapjunk, ami nem négyzet. Mindkét irány járható. Ha a téglalappal kezdünk, a gyerekek számára természetesebb lesz, hogy minden négyzet téglalap, de figyeljünk arra, hogy a négyzet tulajdonságainál azokat is soroljuk fel, amelyek abból fakadnak, hogy téglalap. Hasonló a probléma kocka - téglatest esetén. A térgeometria egyébként is sok nehézségeket okoz a gyerekeknek, ezért célszerű az egyszerűbb problémákkal kezdeni, a kockával, a kockákból épített testeken bemutatni a hálókat, nézeteket, építéseket, térfogatot, felszínt, még akkor is, ha egyébként a definícióknál a téglatesttel kezdtünk.
A következőkben a speciális négyszögek bevezetésére mutatunk egy tevékenységet papírcsíkok alkalmazásával. A papírcsíkok tulajdonsága, hogy a két széle párhuzamos.
Trapézok: Egy papírcsíkból vagdossunk le különböző négyszögeket!
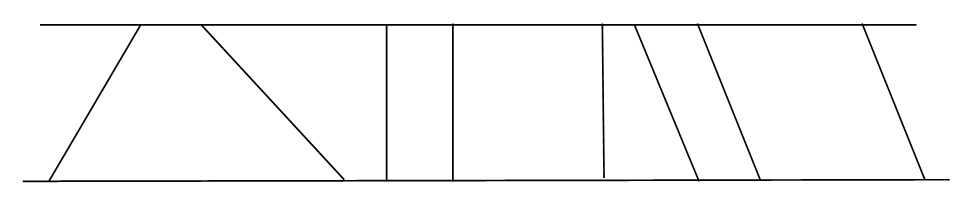
A levágott négyszögek mind trapézok, és speciálisan van köztük téglalap, négyzet, (paralelogramma, rombusz).
Paralelogramma: két különböző szélességű papírcsíkot fektessünk ferdén egymásra.
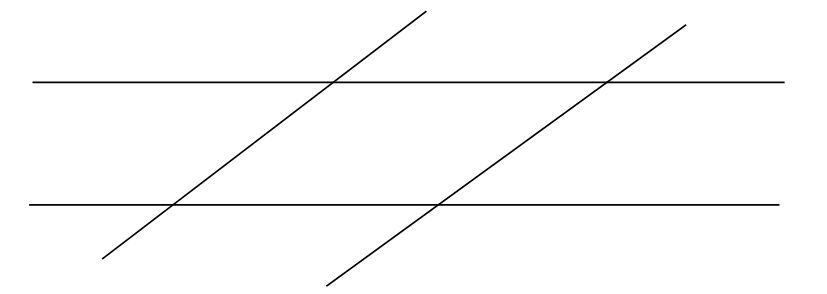
A két papírcsík metszete a paralelogramma.
Ha a két papírcsík merőleges egymásra, akkor metszetük téglalap, tehát minden téglalap paralelogramma.
Ha a két papírcsík egyforma szélességű, akkor metszetük rombusz, tehát minden rombusz paralelogramma.
Ha a két egyforma szélességű papírcsík merőleges egymásra, akkor a metszetük négyzet, tehát minden négyzet rombusz és téglalap is egyben.
Problémát szokott okozni a húrtrapéz elnevezés használata. A húrtrapéz az a tengelyesen szimmetrikus trapéz, amelynek van nem csúcson átmenő szimmetriatengelye. A húrtrapéz elnevezés abból adódik, hogy kör írható köré. Nem nevezhetjük egyenlő szárú trapéznak, mert a paralelogramma is egyenlő szárú trapéz, és szimmetrikus trapéznak sem, mert a rombusz is az.
A speciális négyszögek definícióját 5-6. osztályban érdemes az oldalakra vonatkozó összefüggések alapján megadni, majd a különböző származtatások alapján megadni a tulajdonságokat, ez könnyebb a gyerekek számára.
Például a deltoid definíciója a transzformációk alapján:
Deltoidnak nevezzük azt a négyszöget, amelynek van csúcson átmenő szimmetria tengelye.
Az oldalak alapján:
Deltoidnak nevezzük azt a négyszöget, amelynek két-két szomszédos oldala egyenlő hosszúságú. A deltoidot a tengelyes tükrözés nélkül is megkaphatjuk, ha két-két egybevágó derékszögű háromszögből rakunk össze különböző négyszögeket.