6.1. Maradékokkal számolás

A gyerekek a számok többszörösei mellett tapasztalatot szereznek azokról a számokról is, amelyek adott számmal osztva ugyanazt a maradékot adják. Ezek a számok egy maradékosztályba tartoznak.

A következő szemléltetés a számegyenes feltekerésével a maradékosztályokat mutatja.

http://tananyag.geomatech.hu/b/508689#material/763837

Óra matematika

Példa: Most déli 12 óra van. Süthet-e a nap 134 óra múlva?

Megoldás: 24 óra múlva újra dél lesz, 24 többszöröse óra múlva is újra dél lesz, így 5·24 óra múlva is dél lesz. 134 = 5 · 24 + 14. Dél után 14 óra múlva hajnali 2 óra lesz, tehát nem süthet a nap.

Itt egy maradékosztályba tartoznak azok a számok, ahány óra múlva újra dél lesz. Így 24 maradékosztály van. A 134 ugyanabba a maradékosztályba tartozik, mint a 14.

Hasonló feladatokat alkothatunk a hét napjaira, a hónapokra, évszakokra vonatkozóan.

Az óra matematika játszható az alábbi oldalon:

http://tananyag.geomatech.hu/b/508731#material/953389

Tekintsük azt a relációt, mely szerint azok a természetes számok vannak egymással relációban, amelyek ugyanazt a maradékot adják n-nel osztva. Ez ekvivalencia reláció, és az osztályozás, amelyet meghatároz, adja a maradékosztályokat. A maradékokkal számolás alapja, hogy ez a reláció kongruencia reláció, a művelet eredményének maradéka a tagok maradékaiból számolható.

Például a 3-as maradékosztályok műveleti táblái:

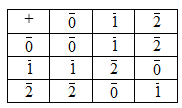
A számolásnál nem számít, hogy az egy maradékosztályba tartozó elemek közül melyikkel dolgozunk.