9.2. A törtfogalom előkészítése
A szemléleti alapozás időszakában konkrét dolgok törtrészeivel foglalkozunk. Ezen a tapasztalatok alapján 5-6. osztályban alakul absztrakció útján a törtszám fogalma.
2. osztályban a részekre osztás tanításakor konkrét tárgyi tevékenységgel előkerül a felezés, negyedelés, hajtogatással, alma szétosztásával megmutatjuk a nyolcad részt is.
Példa: A zöld (12) rudat rakjuk ki csupa piros és csupa rózsaszín rúddal!
Megoldás: A pirosból 3 rúd teszi ki a zöldet, ezért a piros a zöld harmada. Rózsaszín rúdból 6 teszi ki a zöldet, ezért a rózsaszín a zöld hatoda.
A kirakásból megtapasztalhatják a gyerekek, hogy a zöld hatoda fele a harmadának.
Itt természetesen a színes rudak hosszáról van szó, ami akkor is érthető a gyerekeknek, ha kicsit pontatlanul nem mondjuk hozzá.
Az osztás és a szorzás kapcsolatát is megfogalmazzuk a fele, stb. kifejezésekkel:
A világoskék rúd fele a lilának, a lila rúd kétszerese a világoskéknek.
Figyeljünk a szóhasználatra, a fél alma mennyiséget jelent, az alma fele pedig az almadarabnak az egészhez való viszonyát.
A mértékegységváltáskor a tízszerezésről és a tizedelésről szerezhetnek tapasztalatot a gyerekek a liter – deciliter, méter – deciméter kapcsolatoknál.
3. osztályban az egységtörtekkel, azaz az 1 számlálójú törtekkel foglalkozunk.
- Törtrészek konstruálása tevékenységgel: Először a megfelelő törtrészeket hozzuk létre tevékenységgel.
- Törtrészek jelölése: Az 1 egésznek a fele 1 ketted rész, a harmada 1 harmad rész, stb.
- Törtrészek felismerése: Különböző dolgokat, rajzokat választunk 1 egésznek, ezeken ismerjük fel a különböző törtrészeket, először a feleket, majd a harmadokat, stb.,
- Törtrészek alkotása: a gyerekek maguk is alkotnak megadott törtrészeket változatos formában. A sok vizuális tapasztalat segíti a tanulókat abban, hogy ránézésre is felismerjék a törtrészeket, ez itt ugyanolyan fontos, mint a darabszámok felismerésénél!
Az alábbi oldalon gyakorolható a törtrészek felismerése és ábrázolása:
http://tananyag.geomatech.hu/b/508649#material/704419
Az 1 negyed többféle ábrázolása:
Figyeljünk arra, hogy vannak olyan elrendezések, amelyeknél a törtrészek megállapítása már inkább csak számolással lehetséges, ránézésre nem.
Vizuálisan az első két ábrán könnyen látható, hogy a téglalap területének 1 negyede van beszínezve. A harmadik ábra a második soronkénti elcsúsztatásával adódik. A negyedik pedig a harmadik ábra soraiban levő piros téglalapok szétcsúsztatásával keletkezik. Ezt azonban nem könnyű észrevenni, ezért számolással is meghatározható, hogy a téglalap 32 mezője közül 8 piros, a
- A törtrészek közötti nagyságrendi kapcsolatok felismerése:
Ha több egyenlő részre vágjuk az egy egészet, akkor egy rész kisebb lesz:
1 egész > 1 ketted > 1 harmad > 1 negyed > 1 ötöd.
- A törtrészekre vonatkozó szöveges feladatok is segítik a fogalom előkészítését.
Adott mennyiség törtrészét kell kiszámolni egységtörtek esetén.
Példa: Peti 12 palacsintát evett. A palacsinták fele kakaós, harmada diós, a maradék túrós volt. Hány palacsintát evett Peti az egyes fajtákból?
Megoldás:
A kakaós palacsinták száma: 12 : 2 = 6.
A diós palacsinták száma: 12 : 3 = 4.
Maradt 12 – 6 – 4 = 2 túrós palacsinta.
4. osztályban már az egységtörtek többszöröseit is bevezetjük, a felépítés a 3. osztályhoz hasonló.
- Tevékenységgel előállítjuk az egységtörtek többszöröseit.
- Jelölések: 1 egész = 2 ketted = 3 harmad = 4 negyed …
Először 3 negyed alakban ismerkednek a gyerekek azzal a nehézséggel, hogy tudniuk kell, hogy a negyed azt jelenti, hogy az 1 egészet 4 egyenlő részre osztjuk, a 3 pedig megmutatja, hogy az egyenlő részek közül hányat veszünk. Ez az írásmód megkönnyíti a gyerekek számára a tört számlálójának és nevezőjének elkülönítését az alapozás időszakában, ezért nem érdemes siettetni a törtvonalas írásmód: 
bevezetését. Az már akkor fontos, amikor a gyerekek számára a tört szám lesz, ami inkább 5. osztályban következik be.
- Hogyan kérdezzünk?
Hányszorosa a
A 2-t 3-mal kell megszorozni, hogy 6 legyen.
Hányadrésze a
A 2-t 3-mal kell megszorozni, hogy 6 legyen., vagy másképp a 6-ot 3-mal kell osztani, hogy 2 legyen.
Ugyanez törtekkel kifejezve problémát jelent:
Hányadrésze a 
-edrésze (kimondva: hatnegyededrésze)a 6-nak.
Ugyanis a 4-et -del kell megszorozni, hogy 6 legyen.)
Amikor a törtrészeket törtekkel fejezzük ki, eltérünk a nyelvtani következetességtől:
A 
része a 6-nak, ami azt jelenti, hogy a 4-et -dal osztani kell, hogy 6 legyen, vagy másképp a 6-ot -dal kell szorozni, hogy 4 legyen. (A kérdésre adott válasz egy szám, ami eddig az osztót jelentő szám volt, de most a tört nevezőjébe került, így ezzel a törtszámmal való szorzást kell végezni az osztás helyett.)
rész = -edrész
A törtrészek tanításakor lényeges lesz, hogy a gyerekek lássák, hogy egy mennyiség része a -szorosa.
A gyerekek számára a probléma sokszor úgy jelenik meg, hogy a „hányszorosa” kérdőszó szorzásra utal,”hányadrésze” kérdőszó osztásra utal, az egységtörtek többszöröseinél azonban szorzás és osztás is szerepel, és ez megzavarhatja a tanulókat. Megfelelne a „Hány hányadrésze” kezdetű kérdés, de nem szokás ezt alkalmazni.
A fenti probléma elkerülése végett szokás a következőképpen kérdezni:
Mekkora része a
- Törtrészek felismerése, majd alkotása változatos formában. Igyekezzünk sokféle mennyiség törtrészeivel kapcsolatos tevékenységeket tervezni. A ránézéses, számolás nélküli látása az egységtörtek többszöröseinek a legfontosabb készség, amit a gyerekekben ebben a témában ki kell alakítanunk.
A törtrészek rajzának felismerése gyakorolható az alábbi játékkal:
http://www.umapalata.com/design_en/games/AZartTOPO.asp?file=AZartTOPO.swf
- Az ábrázolás segítségével összehasonlítunk azonos nevezőjű és azonos számlálójú törteket: 
.
- Az adott törtrészeket 1 egészre kiegészítő törtrészek alkotása.
Gyakorolható például az alábbi játékkal:
http://www.umapalata.com/design_en/games/AZartALL.asp?file=AZartALL.swf
- Szemléltetjük egyszerű törtek bővítését azzal, hogy az egy egészet több részre vágjuk.
- Mutatunk 1-nél nagyobb törteket is:
- Szöveges feladatok:
Törtrészek kiszámítása egységtörtek többszörösei esetén:
Példa: Kati a 240 Ft-jának részén csokoládét vásárolt. Mennyit fizetett a csokoládéért?
Megoldás: Ábrázoljuk egy szakasszal Kati pénzét, és jelöljük a részét!
Egy szakasz a pénzének negyedének felel meg: 240 : 4 = 60 Ft-nak.
Kati pénzének a részének 3 szakasz felel meg, ez: 3 · 60 = 180 Ft-ot ér.
Egészrész kiszámítása:
Peti elköltötte a pénzének az 
részét, így 300 Ft-ja maradt. Mennyi pénze volt eredetileg?
Megoldás: Ábrázoljuk egy szakasszal Peti pénzét, és jelöljük az elköltött részt:
Az ábráról leolvashatjuk, hogy a megmaradt 
része, 2 szakasznak felel meg.
Így a pénz része egy szakasz: 300 : 2 =
Az egész pénz 3 szakasz: 3 · 150 =
Tipikus hiba a fenti feladat megoldásában, hogy a gyerekek a megmaradt 300 Ft-ot szorozzák 3-mal az egy egész meghatározásához. Ez a harmad kulcsszóval jelzett művelet formális megfordítása lenne, itt azonban a maradék adott, ezért nem helyes.
A törtrészekkel kapcsolatos szöveges feladatokban a törtrészeket szakaszokkal ábrázoljuk, majd a szakaszokról leolvasott összefüggések alapján következtetünk.
5. osztályban a törtek kétféle értelmezése közül az első még az alsó tagozatos törtrész értelmezésnek felel meg, de már nagyobb számokkal a szemlélettől elszakadva is használjuk.
1. értelmezés: A tört nevezője megnevezi, hogy az 1 egészet hány egyenlő részre osztjuk.
A tört számlálója megmutatja, hogy az egyenlő részek közül hányat veszünk.
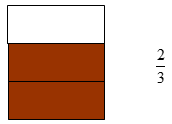
2. értelmezés: A tört a 2 egésznek a harmada:
A második értelmezés közelebb visz ahhoz, hogy a törtrészből törtszám legyen: = 2 : 3.
Ezzel a pozitív racionális számokat vezetjük be két pozitív egész szám hányadosaként, amelyeknek előbbi, törtvonallal felírt alakját közönséges tört alaknak mondjuk, a helyiérték-táblázat alapján tizedes vesszővel írt alakját tizedes tört alaknak (a tizedes törtek alsó tagozatban nem fordulnak elő, ezért ezekkel nem foglalkozunk).
5. osztályban már az időhiány miatt jóval kevesebb manipulatív és képi tapasztalatot szereznek a gyerekek a törtekkel kapcsolatos ismeretek absztrakciójához, ezért elengedhetetlen az alsó tagozatos sok szemléltetés.
Például a 
< 1 relációt még könnyen el tudják képzelni, de a 
< 1 reláció felismerése már absztrakciót igényel, ami nem lehetséges megfelelő mennyiségű konkrét tapasztalat nélkül. Sok gyereknek azért van problémája a törtekkel, mert nem elégséges alapozás után kényszerült absztrakcióra.