13.2. Halmazok

A halmazokkal kapcsolatos tevékenységeket egy, majd több szempont szerinti válogatásokkal kezdjük.

Adott egy alaphalmaz, ennek elemeiből válogatjuk ki az elemeket egy halmazba.

A halmaz elemeit megadhatjuk valamilyen tulajdonsággal, vagy az elemek felsorolásával. Az alaphalmaz azon elemei, amelyek nem tartoznak a halmazba a halmaz komplementer, vagy kiegészítő halmazát alkotják.

Válogatás két szempont alapján az alaphalmaz elemeiből. A feladatok nehézségi sorrendje a következő:

- Először olyan halmazokat adjunk meg, amelyeknek nincs közös eleme, azaz diszjunktak.

Például a logikai készlet elemei közül az egyik halmazba a kicsi, a másikba a nagy elemek kerülnek.

- A két adott halmaz közül az egyik részhalmaza a másiknak, azaz az egyik halmaz minden eleme a másik halmaznak is eleme. Ezzel nagyon fontos kapcsolatot gyakorolhatnak a gyerekek, a tartalmazás relációt, ami a fogalmak hierarchiáját, az általános, és speciális fogalmak kapcsolatát segít megérteni.

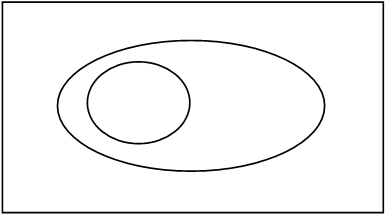
Például a négyzetek halmaza részhalmaza a téglalapok halmazának.

- A két halmaz. Nevezzük meg az egyes halmazrészekbe tartozó elemek tulajdonságait. Például, tartozzanak az  halmazba a kék, a  halmazba a kör alakú elemek!

Két halmaz közös része, vagy metszete az a halmaz, melynek pontosan azok az elemei, amelyek mindkét halmaznak elemei . A példában ezek azok az elemek, amelyek kékek és körök.

A baloldali halmazrész az  és a  halmazok különbsége, az a halmaz, amelynek pontosan azok az elemei, amelyek az A halmazban benne vannak, a B halmazban nincsenek benne . A példában ezek azok az elemek, amelyek kékek, de nem körök, vagyis a kék négyzetek és a kék háromszögek (lehetnek kicsik vagy nagyok, lyukasak vagy nem lyukasak).

A jobboldali halmazrész a  és az  halmazok különbsége, az a halmaz, amelynek pontosan azok az elemei, amelyek a  halmazban benne vannak, az A halmazban nincsenek benne . A példában ezek azok az elemek, amelyek körök, de nem kékek, vagyis a piros, sárga vagy zöld körök (lehetnek kicsik vagy nagyok, lyukasak vagy nem lyukasak).

A két halmaz egyesítése vagy uniója az a halmaz, melynek pontosan azok az elemei, amelyek legalább az egyik halmaznak elemei . A példában ezek azok az elemek, amelyek kékek vagy körök.

A két halmazon kívüli elemek sem az , sem a  halmazban nincsenek benne . A példában ezek azok az elemek, amelyek se nem körök, se nem kékek.

A halmazok és a logika itt együtt fordul elő:

A két halmaz metszetében levő elemekre igaz az állítás, hogy kékek és körök.

A két halmaz egyesítésében levő elemekre igaz az állítás, hogy kékek vagy körök.

Az elemek két halmazba rendezése gyakorolható az alábbi oldalon:

http://tananyag.geomatech.hu/b/508027#material/703889

Válogatás három szempont alapján

4. osztályban már három szempont alapján is csoportosíthatjuk az alaphalmaz elemeit. Itt is hasonló a nehézségi sorrend a két szempont szerinti halmazba rendezéshez, előbb diszjunkt (közös elem nélküli) halmazokba soroljuk az elemeket, majd a halmazok tartalmazzák egymást, végül általánosan bármely két halmaznak van közös része, és a három halmaznak is.

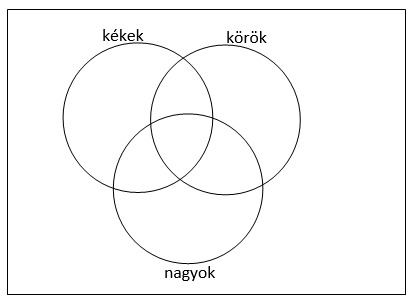
Logikai szita

Számoljuk meg a halmazok, és az egyes halmazrészek elemszámát!

Példa: A kezemben van 7 elem a logikai készletből, 5 kicsi és 4 kör. Hogy lehet ez?

A kérdés hamar megoldódik, ugyanis annak ellenére, hogy 5 + 4 > 7, mégis lehetséges az elemek kiválasztása, hiszen a kicsi körök a kicsik és a körök halmazába is beleszámítanak. Így több lehetséges megoldás adódik, például van 2 kicsi kör, 2 kicsi háromszög, 1 kicsi négyzet, 2 nagy kör, és nincs olyan elem, amelyik se nem kicsi, se nem kör.

A logikai szita azt jelenti, hogy két halmaz egyesítésének elemszámát úgy kapjuk, hogy a két halmaz elemszámának összegéből kivonjuk a metszetük elemszámát. Ugyanis a metszetbe tartozó elemeket mindkét halmaz elemszámánál figyelembe vettük.

A logikai szita formula három halmazra a következő:

Ha három halmaz egyesítésének elemszámát számoljuk, először összeadjuk a három halmaz elemszámát. Ekkor azokat az elemeket, amelyek két halmazban is benne vannak, duplán számoltuk, ezért ezeket le kell vonni, azaz kivonjuk az összes lehetséges halmaz elemszámát, amely halmazok két halmaz metszeteként állnak elő. Ekkor a három halmaz metszetében levő elemeket háromszor hozzáadtuk, de háromszor le is vontuk, ezért egyszer hozzá kell adni.