11.3. Egyenletek
Ha a nyitott mondatban egyenlőségjel szerepel, akkor a nyitott mondat tekinthető egyenletnek. A nyitott mondat igazsághalmazának keresése az egyenlet megoldása.
Egyenlet megoldása lebontogatással:
A módszer alapja a visszafelé következtetés.
Gondoltam egy számra, megszoroztam 2-vel, és a szorzathoz hozzáadtam 3-at, így 15-öt kaptam. Melyik számra gondoltam?
A megoldást visszafelé gondolkodással a buborékos ábra szemlélteti:
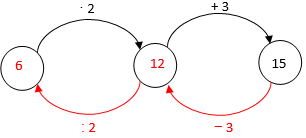
Felírhatunk egyenletet: 2x + 3 = 15.
A visszafelé gondolkodást követve a megoldás:
Először a 2x-et keressük, ezt jelölhetjük is az egyenleten: 2x + 3 = 15
Melyik az a szám, amelynél 3-mal nagyobb szám a 15? Ez a 15 – 3 = 12.
Vagy: ha a 2x-hez nem adtam volna 3-at, akkor 3-mal kevesebb, vagyis 12 lenne.
Így a 2x = 12 egyenlethez jutunk.
x-et keressük:
Melyik az a szám, amelynek 2-szerese 12? Ez a 12 : 2 = 6.
Ha az x-et nem szoroztam volna meg 2-vel, akkor 6 lenne.
Tehát x = 6.
A lebontogatás módszerét csak akkor alkalmazhatjuk, ha az egyenletben egy helyen szerepel az ismeretlen. Mivel a műveletek megfordítására épül, ezért már 5-6. osztályban is tanítják, azonban a mérlegelv megismerése után okafogyottá válik.
Alsó tagozatos példa a mérlegelv előkészítésére
A piacon két görögdinnyéért és egy sárgadinnyéért adnak 3 cukkinit és egy főzőtököt. Egy főzőtökért egy sárgadinnyét és egy cukkínit adnak. Hány cikkínit adnak egy görögdinnyéért, ha az egyes zöldségek mindig ugyanannyit érnek?
Rajzoljuk le a zöldségeket mérlegeken!
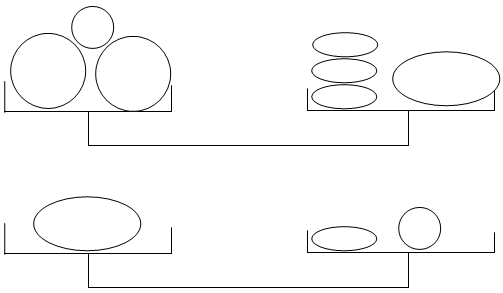
A felső mérlegen levő főzőtök helyére tegyünk egy cukkínit és egy sárgadinnyét!

Ha a mérleg mindkét serpenyőjéből elveszünk egy sárgadinnyét, akkor az egyensúly megmarad.

A jobboldalon a cukkíniket két egyenlő részre osztva látható, hogy egy görögdinnye két cukkínit ér.

A gyerekek konkrét tárgyi tapasztalatokat szerezhetnek a kétkarú mérleggel való méregetésről, az összefüggések megtalálásáról, ha például színes rudakat méregetünk. Ezután a fentihez hasonló példákat oldhatunk meg rajzok segítségével.
A mérleggel megoldott feladatokkal a következő tapasztalatokat szerezhetjük meg:
A mérleg két serpenyőjének egyensúlya megmarad, ha
- a mérleg mindkét serpenyőjéből ugyanakkora tömeget elveszünk;
- a mérleg mindkét serpenyőjéhez ugyanakkora tömeget hozzáteszünk;
- a mérleg mindkét serpenyőjében levő tömeget megszorozzuk ugyanazzal a 0-tól különböző számmal;
- a mérleg mindkét serpenyőjében levő tömeget elosztjuk ugyanazzal a 0-tól különböző számmal.
Ezek az átalakítások lesznek az egyenletek megoldásánál az ekvivalens átalakítások.
A fenti példában megjelent a behelyettesítés is, ami később az egyenletrendszer megoldásában lesz hasznos.
Egyenlet megoldása mérlegelvvel
A mérlegelvet konkrét és lerajzolt mérlegeken szerzett tapasztalatokra építjük.
Példa: A mérleg egyik serpenyőjében két zacskó gumicukor és egy 3 dkg-os tömeg van, a másik serpenyőjében pedig öt 3 dkg-os tömeg, és így a mérleg egyensúlyban van. Hány dekagramm egy zacskó gumicukor?
Játsszuk el kétkarú mérleggel, tapasztaljuk meg, milyen változtatásokat végezhetünk úgy, hogy az egyensúly fennmaradjon. Később elegendő rajzzal is szemléltetni:
Az ismeretlen tömegű zacskót körnek rajzoljuk

Vegyünk le a mérleg mindkét serpenyőjéből egy-egy 3 dkg-os tömeget!

A baloldalon két egyenlő tömegű zacskó van, ezért a jobboldalon levő tömegeket is osszuk két egyenlő részre! Ebből látható, hogy egy zacskó tömege két 3 dkg-os tömeggel tart egyensúlyt.

Tehát egy zacskó gumicukor tömege 6 dkg.
Ugyanezek a lépések formálisan:
Egy zacskó gumicukor tömege: x.
Két zacskó tömege: 2x
A baloldali serpenyőben levő tömeg 2x +
2x + 3 = 15
Az x-et keressük, először a 3-at szeretnénk eltüntetni.
Vonjunk ki az egyenlet mindkét oldalából 3-at, ekkor az egyenlőség megmarad.
2x + 3 = 15 / −3
2x + 3 – 3 = 15 – 3
2x = 12 / : 2 Osszuk el az egyenlet mindkét oldalát 2-vel!
2x : 2 = 12 : 2
x = 6
Látható a különbség a lebontogatás és a mérlegelv között. Itt nem a műveletek megfordítására hivatkozunk, a 2x : 2 = x lépés nem olyan egyszerű a gyerekeknek, ha nem formálisan akarjuk tanítani.
A mérlegelv lehetőséget ad arra is, hogy az egyenlet mindkét oldalából az ismeretlent vagy annak többszörösét vonjuk ki, így az egyenlet egyik oldalára rendezhetők az ismeretlenek.
Az ismeretlenekkel végzett műveletek túl absztraktak a 6. osztályosok többsége számára, nem felel meg az életkori sajátosságaiknak. Ezt az is igazolja, hogy az algebrai kifejezések, azaz a betűkkel számolás 7. osztályos tananyag, így enélkül mérlegelvvel egyenletmegoldást tanítani 6. osztályban sérti a tananyagok egymásra épülésének logikáját.
Ne tanítsunk 7. osztály előtt egyenletmegoldást mérlegelvvel!
A szöveges feladatok megoldási tervének felírását gyakran nyitott mondattal várják el a gyerekektől. Sok gyerek ezt a feladat megoldása után írja oda a megfelelő helyre. Ez teljesen természetes ebben a fejlődési szakaszban, hiszen hiába írja fel a helyes nyitott mondatot, rendszerint úgysem fogja tudni megoldani azt. A próbálgatás ritkán jelent teljes megoldást, az egyenletmegoldás többi módszere pedig nem felel meg a gyerekek életkori sajátosságainak, ezért nem alkalmazható. Ezért a szöveges feladatoknál a nyitott mondatok felírása rendszerint felesleges. A matematikai modell ekkor a szakaszos ábrázolás, a buborékos modell, és a megfelelő műveletek felírása, amelyeket szöveggel lehet indokolni.
A szöveges feladat megoldási terveként felírt nyitott mondat gyakran a következő alakú: ∆ = (32 – 8 ) : 2.
Ennek megoldásához valóban nem kell egyenletmegoldás, csupán számítások elvégzése. Fontos azonban, hogy a ∆ jel alkalmazása ne fedje el azt, hogy a szövegben mit jelöl a ∆. Gyakori hiba, hogy egy számítás végén a gyerekek elfelejtik, hogy mit számítottak ki, ebben pedig a ∆ jel alkalmazása nem segíti őket. Hasznosabb, ha szöveggel kiírjuk a műveletsor elé, hogy azzal mit fogunk kiszámítani.