Bevezetés
- C1: Optikai alapok az ELI-ALPS tükrében - MSc
- Bevezető I.
- A lézerfizika alapelvei és bevezetés a nemlineáris optikába I.
- A lézerműködés alapelvei
- Gerjesztett kvantumállapotok spontán emissziója
- Indukált abszorpció és emisszió
- Populácóinverzió és erősítés
- Pozitív visszacsatolás és lézeroszcillációk
- Abszorpció telítődése
- Abszorpció és indukált emisszió, kvázi-klasszikus leírás
- Abszorpciós hatáskeresztmetszet, homogén vonalkiszélesedés
- Abszorpciós hatáskeresztmetszet, inhomogén vonalkiszélesedés
- Vonalkiszélesedést okozó hatások
- Gyakori lézerátmenetek paraméterei
- Rezonátorok
- Pumpálás
- Tesztkérdések I.
- A lézerműködés alapelvei
- A lézerfizika alapelvei és bevezetés a nemlineáris optikába II.
- A lézerfizika alapelvei és bevezetés a nemlineáris optikába III.
- Folytonos üzemű lézerek: rate-egyenletek, 4-nívós séma
- Lézerek hangolása
- Sokmódusú lézeroszcilláció homogén frekvenciakiszélesedés esetén
- Sokmódusú lézeroszcilláció inhomogén frekvenciakiszélesedés esetén
- Transzverzális egymódus-szelekció
- Longitudinális egymódus-szelekció
- Fabry-Perot etalonok, mint módusszelektív elemek
- Egymódus-szelekció egyirányú gyűrűrezonátorok segítségével
- Lézerfrekvencia fluktuációi és frekvenciastabilizáció
- Lézerintenzitás zaja és zajcsökkentés
- Q-kapcsolás
- Móduscsatolás (Mode locking)
- Tesztkérdések III.
- A lézerfizika alapelvei és bevezetés a nemlineáris optikába IV.
- Bevezetés a nemlineáris optikába
- Tesztkérdések IV.
- Az optikai méréstechnika alapjai I. - Az optikai méréstechnika eszközei
- Az optikai méréstechnika alapjai II. - Interferometria
- Az optikai méréstechnika alapjai III. - Fényszórás, polarizáció
- Az optikai méréstechnika alapjai IV.
- Tartalomjegyzék
- Bevezetés
- UV-látható spektroszkópia
- Infravörös spektroszkópia
- Raman spektroszkópia
- Lumineszcencia (fluoreszcencia) spektroszkópia
- Tesztkérdések VIII.
- Vékonyrétegek I.
- Vékonyrétegek II.
- Vékonyrétegek III.
- Vékonyrétegek IV.
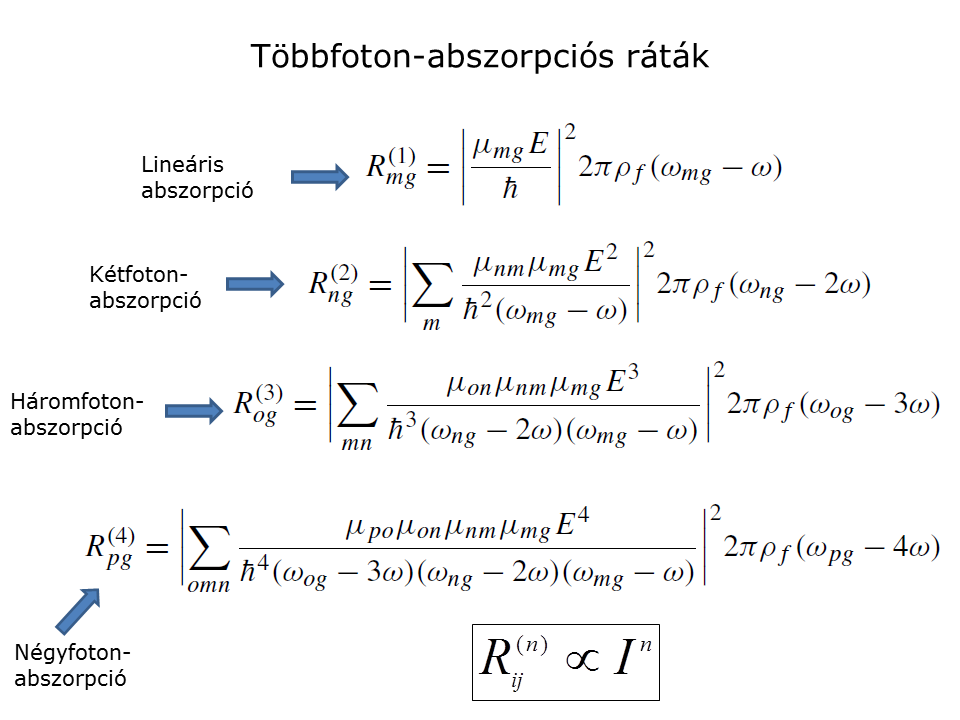
Többfotonos abszorpció és ionizáció
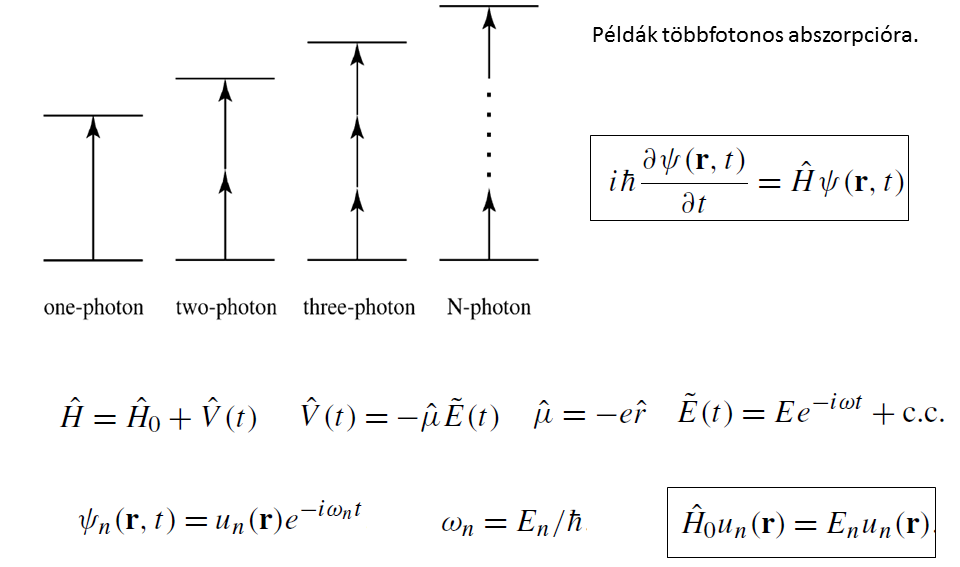
Egy- és többfotonos abszorpciós folyamatok rátáit a következőképp számoljuk. Perturbációs módszerekkel megoldjuk a ψ(r,t) atomi elektron-hullámfüggvényre a Schrödinger-egyenletet, feltételezve, hogy az elektron külső lézertérrel való kölcsönhatási energiája jóval kisebb, mint az elektron és a belső atomi tér kölcsönhatási energiája. H a lézertérben lévő atom Hamilton-operátora, H0 a kölcsönhatásmentes atom Hamilton-operátora, V a külső E(t) térrel való kölcsönhatás energiája, μ az atomi átmenet dipóloperátora. Feltesszük, hogy a lézerteret t=0 időpillanatban kapcsoljuk be. A ψn-ek a kölcsönhatásmentes atom energia-sajátállapotai.