Mie-elmélet

Mie 1908-ban állította fel elméletét, amelyet Lorenz-Mie elméletként is emleget a szakirodalom. Ebben az elektromágneses elméletet felhasználva, a Maxwell egyenletekből kiindulva levezette a kis részecskéken történő fényszórást. A részecskéket homogén gömbként modellezve, és monokromatikus síkhullámként felírt megvilágítást feltételezve levezette a szórási és extinkciós együtthatókat és keresztmetszeteket, valamint a szórt intenzitást a részecske méret, a törésmutató, a megvilágító hullámhossz és a detektálási irány függvényében.
Az an és bn a mérettől és a megvilágító fény hullámhosszától függő szórási együtthatók, x a méretparaméter és m a relatív törésmutató.
Ψ és ξ az n-ed rendű Riccati Bessel függvényeket jelölik. A méretparaméter a részecske törésmutatójának, méretének és a megvilágító hullámhossznak a függvénye.

Qs a teljes Mie szórási együttható vagy szórási hatásfok, amelyet úgy definiálhatunk, mint a részecskéről minden irányban kiszórt fluxusnak és a geometriai keresztmetszeten bejövő fluxusnak a hányadosát. A definícióból is látszik, hogy ez nem független a szórási keresztmetszettől.
Ii a bejövő intenzitást jelöli, r pedig a részecskétől a megfigyelő távolsága. S1 és S2 az irányfüggő szórási együtthatók.
A fenti együtthatók numerikus számolása több problémát is felvet. Egyrészről nagyobb méretparaméter esetén nagy lehet az összegzendő tagok száma. Másrészről a Bessel függvények rekurzív meghatározásánál a nem megfelelő irányú rekurzió és nem megfelelő számú lépés könnyen divergenciához vezethet, ami jelentős hibát okozhat.
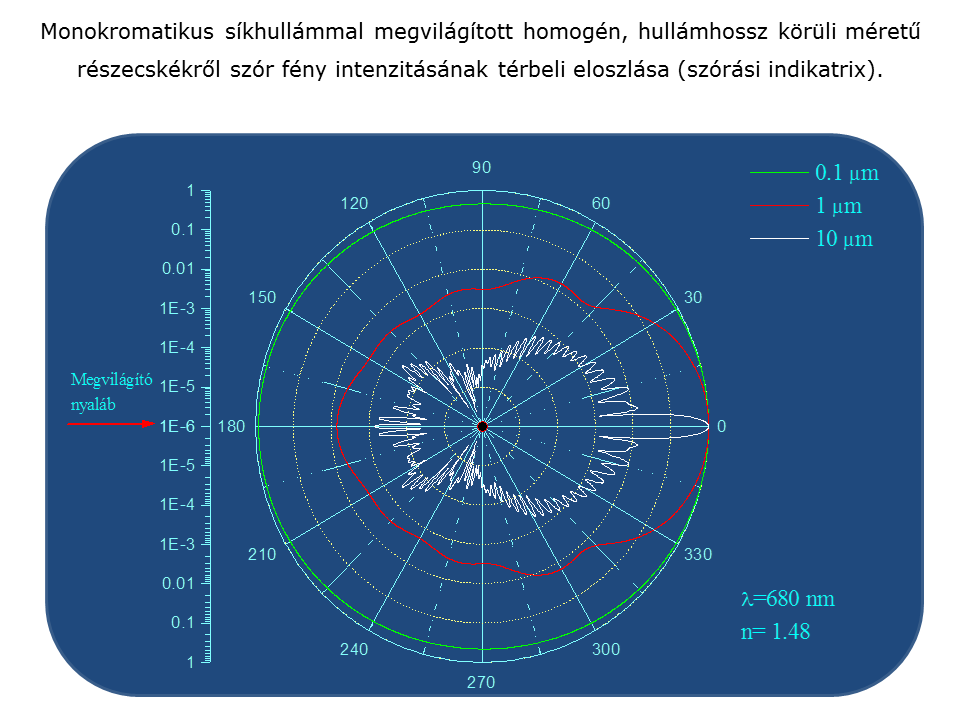
Az ábrán három különböző méretű (0.1, 1, 10 mikrométer átmérőjű) részecskéről szórt fény intenzitásának irányfüggése látható. A különböző méretű részecskék szórása az előreszórásra van normálva, így az szórási indikatrixok alakja összehasonlítható. Az intenzitás logaritmikus skálán van ábrázolva a több nagyságrendet átfogó intenzitás változások miatt.
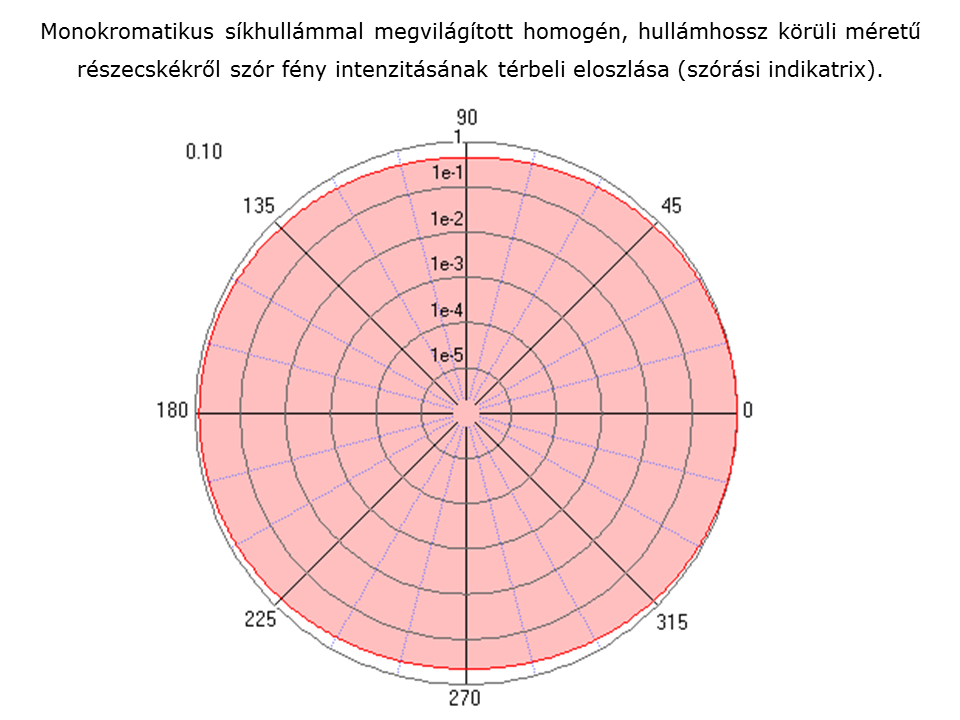
Az ábrán 0.1 és 10 mikrométer közötti méretű részecskéről szórt fény intenzitásának irányfüggése látható animáció formájában. A különböző méretű részecskék szórása az előreszórásra van normálva, így az szórási indikatrixok alakja összehasonlítható. Az intenzitás logaritmikus skálán van ábrázolva a több nagyságrendet átfogó intenzitás változások miatt. Az animáció bal felső sarkában levő szám mutatja az aktuális részecske méretet (átmérőt) mikrométerben.

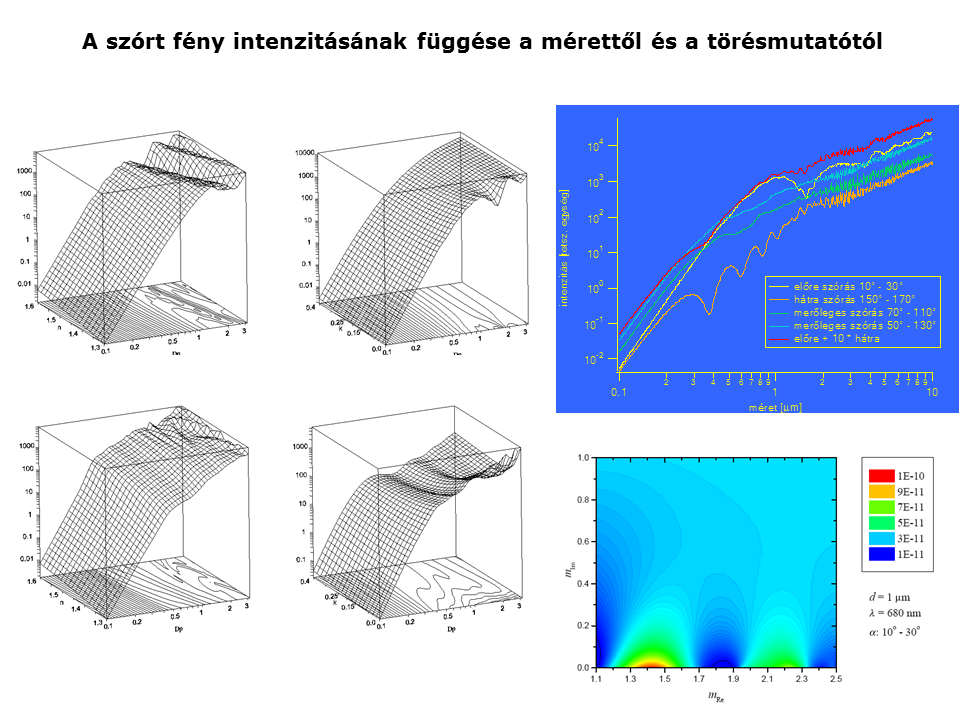
Az előző ábrán felírt integrál megoldásait láthatjuk a részecskék mérete és törésmutatója függvényében.
A baloldali 3D ábrákon az x tengelyen a részecske méret szerepel mikrométerben, az y tengelyen a komplex törésmutató valós része, a z tengelyen pedig a szórt intenzitás különböző geometriák esetén.
A jobboldali 3D ábrákon az x tengelyen a részecske méret szerepel mikrométerben, az y tengelyen a komplex törésmutató képzetes része, a z tengelyen pedig a szórt intenzitás különböző geometriák esetén.
A jobb felső ábra 5 különböző szórási geometriában mutatja be a szórt intenzitás függését a részecske mérettől adott törésmutató mellett.
A jobb alsó ábra pedig egy adott méretű (1 mikronos) részecskéről szórt fény intenzitásának változását mutatja be a komplex törésmutató függvényében.
Ezekből jól látszik, hogy a szórás nem monoton függvénye sem a részecske méretnek sem a törésmutatónak.
Mindig az adott alkalmazáshoz kell megtalálni a megfelelő szórási geometriát.