Abszorpció és indukált emisszió, kvázi-klasszikus leírás

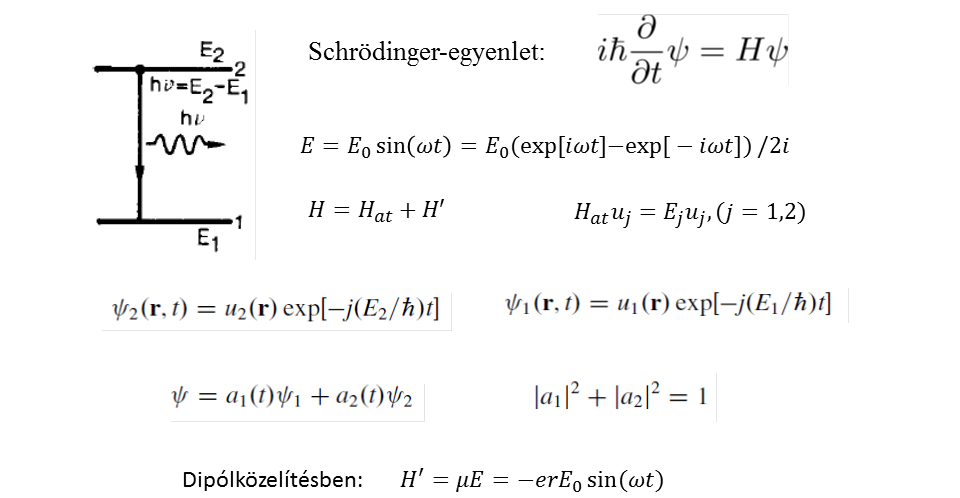
Számítsuk ki az atomi átmeneti valószínűségeket a kvázi-klasszikus leírás keretein belül! Eszerint az atomot kvantummechanikailag (a hulllámfüggvényt Schrödinger-egyenlettel jellemezve), az elektromágneses teret pedig klasszikus objektumként kezeljük. Hat az atomi Hamilton-operátor az elektromágneses tér hiányában, H’ pedig a kölcsönhatási Hamilton-operátor, a₁ és a₂ a megfelelő atomi nívókhoz tartozó valószínűségi amplitúdók, melyek abszolútérték-négyzete megmutatja, milyen valószínűséggel található az atom az adott állapotban. µ az atomi dipóloperátor.

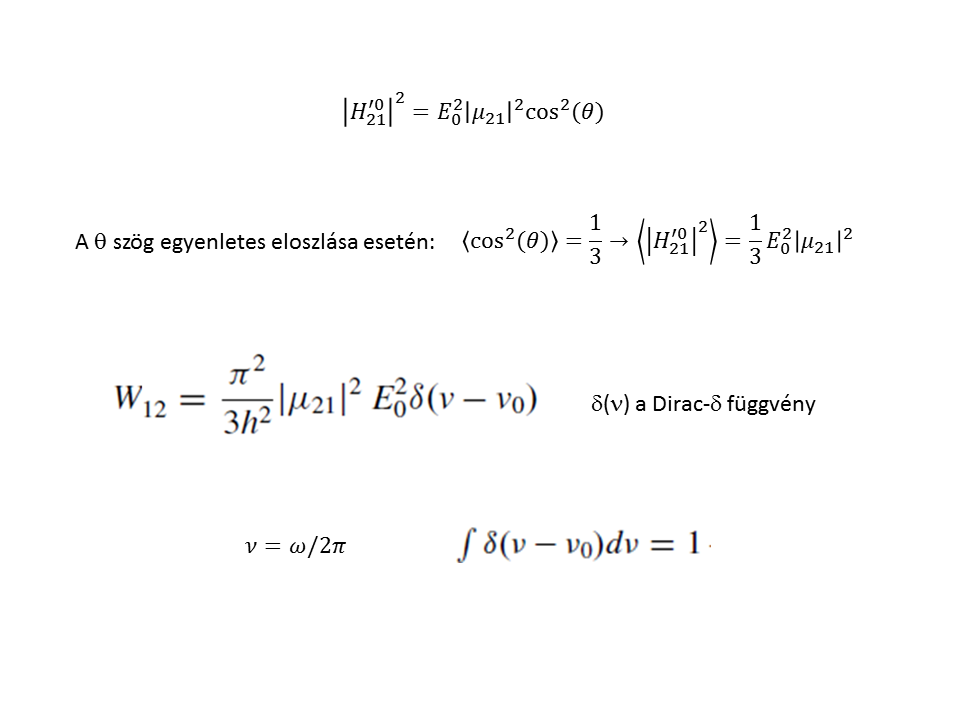
θ a μ és E₀ által bezárt szög. Vegyük észre, hogy az abszorpciós valószínűségre kapott kifejezés nem fizikális, mivel Dirac delta függvényt tartalmaz, mely rezonancia esetén szinguláris, rezonancián kívül pedig nulla értékkel bír (integrálja pedig egységnyi). Ez arra a feltevésre vezethető vissza, hogy kezdetben feltettük: az elektromágneses tér és az atom kölcsönhatása zavartalanul folytatódhat önkényesen hosszú ideig.

Számos zavaró folyamat akadályozza meg, hogy atom és tér tetszőlegesen hosszú ideig hasson kölcsön (pl. spontán emisszió, egyéb atomokkal vagy fononokkal való ütközés, stb.). Ezeket a mechanizmusokat (ld. később) figyelembe véve, a Dirac delta függvényt Lorentz-függvény váltja fel az abszorpció valószínűségére vonatkozó kifejezésben. Az abszorpciós és indukált emissziós ráták megegyeznek egymással.