8.1. Középpontos hasonlóság
Adott egy ![]() pont (középpont), és egy
pont (középpont), és egy ![]() valós szám (arány). Az
valós szám (arány). Az ![]() középpontú,
középpontú, ![]() arányú középpontos hasonlóságot a következőképpen definiáljuk:
arányú középpontos hasonlóságot a következőképpen definiáljuk: ![]() pont képe önmaga, minden más
pont képe önmaga, minden más ![]() pont képe az a
pont képe az a ![]() pont az
pont az ![]() félegyenesen, amire
félegyenesen, amire ![]() .
.
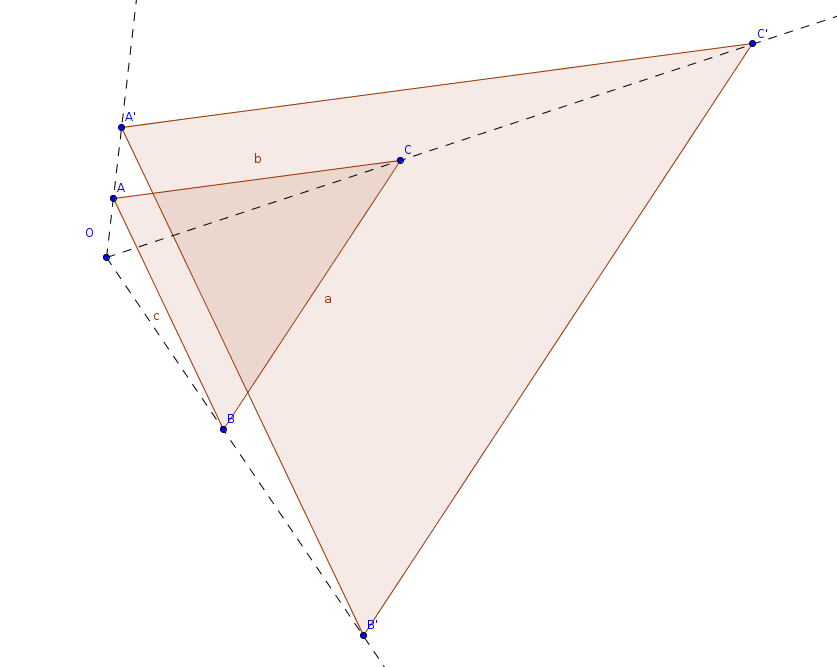
Tekintsük meg a középpontos hasonlóságot szemléltető dinamikus ábrát a GeoGebraTube-on.
A következő tételben összegyűjtöttük a középpontos hasonlóság legfontosabb tulajdonságait. Ez a tétel lényegében a párhuzamos szelőkről és szelőszakaszokról 4.2. szakaszban elmondottak következménye.
21. tétel. A középpontos hasonlóság
- aránytartó, egy
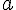 hosszúságú szakasz képe
hosszúságú szakasz képe  ;
; - szögtartó;
- párhuzamos egyenesekpárokat párhuzamos egyenespárokba visz;
- a középpontra illeszkedő egyeneseket invariánsan hagyja.
Ha ![]() (középpontos) nagyításról,
(középpontos) nagyításról, ![]() esetén (középpontos) kicsinyítésről beszélünk. Szokás értelmezni a középpontos hasonlóságot
esetén (középpontos) kicsinyítésről beszélünk. Szokás értelmezni a középpontos hasonlóságot ![]() arány esetén is, ilyenkor először végrehajtunk egy
arány esetén is, ilyenkor először végrehajtunk egy ![]() arányú középpontos hasonlóságot a korábban leírtak szerint, majd tükrözünk középpontosan
arányú középpontos hasonlóságot a korábban leírtak szerint, majd tükrözünk középpontosan ![]() -ra.
-ra.
A kerület, terület és a középpontos hasonlóságok kapcsolatát vizsgálja a következő feladat.
8.1. gyakorlat. a) Egy négyzet oldalait kétszeresére növeljük. Hogyan változik a kerülete és a területe?
b) Egy négyzet oldalait ![]() -szorosára növeljük. Hogyan változik a kerülete és a területe?
-szorosára növeljük. Hogyan változik a kerülete és a területe?
Megoldás. a) A kerület kétszeresére, a terület négyszeresére nő.b) A kerület ![]() -szorosára, a terület
-szorosára, a terület ![]() -szeresére változik. Tekintsük meg az illusztráló dinamikus ábrát.
-szeresére változik. Tekintsük meg az illusztráló dinamikus ábrát. ![]()
A fentiek alapján világos, de precízen már azért nehezebben igazolható a következő tétel.
22. tétel. Ha egy ![]() lemezt
lemezt ![]() -szorosára nagyítunk/kicsinyítünk, kerülete
-szorosára nagyítunk/kicsinyítünk, kerülete ![]() -szorosára, területe
-szorosára, területe ![]() -szeresére változik.
-szeresére változik.
A térbeli analógia is világos.
8.2. gyakorlat. a) Egy kocka éleit háromszorosára növeljük. Hogyan változik a felszíne és a térfogata?
b) Egy kocka éleit ![]() -szorosára növeljük. Hogyan változik a felszíne és a térfogata?
-szorosára növeljük. Hogyan változik a felszíne és a térfogata?
c) Egy testet ![]() -szorosára nagyítunk/kicsinyítünk, hogyan változik a felszíne és térfogata?
-szorosára nagyítunk/kicsinyítünk, hogyan változik a felszíne és térfogata?