7.3. Tengelyes szimmetriák
7.5. feladat. Egy ![]() korlátos alakzat tengelyesen szimmetrikus az
korlátos alakzat tengelyesen szimmetrikus az ![]() és
és ![]() egyenesekre vonatkozóan is. Igaz-e, hogy ekkor szimmetrikus az
egyenesekre vonatkozóan is. Igaz-e, hogy ekkor szimmetrikus az ![]() egyenesre is, ahol
egyenesre is, ahol ![]() az
az ![]() egyenes
egyenes ![]() -re vett tükörképe? Indokoljunk részletesen, vagy adjunk ellenpéldát!
-re vett tükörképe? Indokoljunk részletesen, vagy adjunk ellenpéldát!
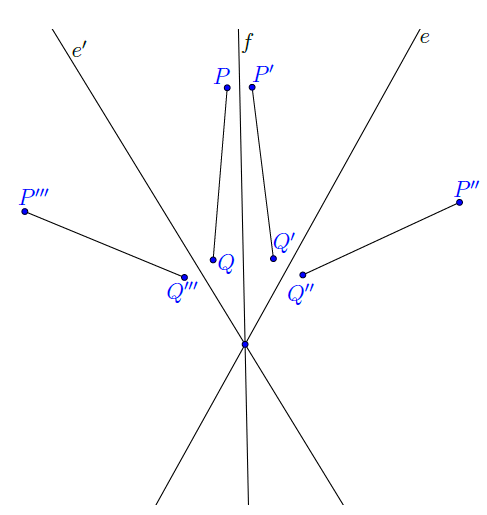
Megoldás. Legyen ![]() pont tetszőleges. Tükrözzük
pont tetszőleges. Tükrözzük ![]() -t először
-t először ![]() -re, a kapott pontot tükrözzük
-re, a kapott pontot tükrözzük ![]() -re, majd a kapott pontot újfent tükrözzük
-re, majd a kapott pontot újfent tükrözzük ![]() -re. Azt állítjuk, hogy az így kapott pont éppen
-re. Azt állítjuk, hogy az így kapott pont éppen ![]()
![]() -re vonatkozó tükörképe. Ennek a ténynek az igazolását az olvasóra bízzuk (16. ábra ill. a vonatkozó dinamikus ábra).
-re vonatkozó tükörképe. Ennek a ténynek az igazolását az olvasóra bízzuk (16. ábra ill. a vonatkozó dinamikus ábra).
Ebből viszont a kérdésre pozitív válasz következik, hiszen az ![]() -re vonatkozó tükrözés helyettesíthető három tükrözés egymásutánjával (rendre
-re vonatkozó tükrözés helyettesíthető három tükrözés egymásutánjával (rendre ![]() -re,
-re, ![]() -re majd
-re majd ![]() -re tükrözünk), amelyek külön-külön mind invariánsan hagyják
-re tükrözünk), amelyek külön-külön mind invariánsan hagyják ![]() -t.
-t. ![]() korlátossága nem lényeges feltevés.
korlátossága nem lényeges feltevés.![]()
7.6. feladat. a) Egy ![]() korlátos alakzatnak pontosan két szimmetriatengelye van. Igazoljuk, hogy ezek egymásra merőlegesek!
korlátos alakzatnak pontosan két szimmetriatengelye van. Igazoljuk, hogy ezek egymásra merőlegesek!
b) Egy ![]() korlátos alakzatnak páros sok szimmetriatengelye van. Igazoljuk, hogy
korlátos alakzatnak páros sok szimmetriatengelye van. Igazoljuk, hogy ![]() középpontosan szimmetrikus! (Vagyis van egy középpontos tükrözés szimmetriája.)
középpontosan szimmetrikus! (Vagyis van egy középpontos tükrözés szimmetriája.)
Megoldás. a) Legyen a két szimmetriatengely ![]() . Legyen
. Legyen ![]() tükörképe
tükörképe ![]() -re
-re ![]() . 7.5. feladat szerint
. 7.5. feladat szerint ![]() is szimmetriatengely, így vagy
is szimmetriatengely, így vagy ![]() , de akkor
, de akkor ![]() , ami ellentmond feltevésünknek, vagy
, ami ellentmond feltevésünknek, vagy ![]() , amiből
, amiből ![]() azonnal következik.
azonnal következik.
b) Részletes megoldást nem adunk, csak a lényeges gondolatokat közöljük. Ismét csak 7.5. feladatot használjuk. Válasszuk ki ![]() szimmetriatengelyt. A maradék szimmetriatengelyek
szimmetriatengelyt. A maradék szimmetriatengelyek ![]() -re szimmetrikus párokba rendeződnek, de mivel páratlan sokan vannak, így valamelyiknek, mondjuk
-re szimmetrikus párokba rendeződnek, de mivel páratlan sokan vannak, így valamelyiknek, mondjuk ![]() -nek nem jut pár. Az a) részhez hasonlóan következik, hogy
-nek nem jut pár. Az a) részhez hasonlóan következik, hogy ![]() . Ha van két egymásra merőleges szimmetriatengely, akkor az alakzat középpontosan is szimmetrikus.
. Ha van két egymásra merőleges szimmetriatengely, akkor az alakzat középpontosan is szimmetrikus. ![]()
A következő feladatot érdeklődő olvasóink figyelmébe ajánljuk.
7.7. feladat. Egy ![]() korlátos alakzatnak legalább két szimmetriatengelye van. Igazoljuk, hogy az összes szimmetriatengely egy közös ponton halad keresztül!
korlátos alakzatnak legalább két szimmetriatengelye van. Igazoljuk, hogy az összes szimmetriatengely egy közös ponton halad keresztül!
Ötlet. Ha ![]() -nak
-nak ![]() szimmetriatengelye, akkor
szimmetriatengelye, akkor ![]() -nak
-nak ![]() mindkét félsíkjába esik pontja (vagy
mindkét félsíkjába esik pontja (vagy ![]() tartalmazza
tartalmazza ![]() -t). Tegyük fel, hogy az állítás nem igaz, és 7.5. feladat segítségével konstruáljunk olyan szimmetriatengelyt, amire ez nem teljesül. Jegyezzük meg, hogy ha
-t). Tegyük fel, hogy az állítás nem igaz, és 7.5. feladat segítségével konstruáljunk olyan szimmetriatengelyt, amire ez nem teljesül. Jegyezzük meg, hogy ha ![]() nem korlátos, akkor az állítás nem igaz, lásd például az egyenest.
nem korlátos, akkor az állítás nem igaz, lásd például az egyenest.